Neon¶
This chapter focuses on implementing the first kernels using ARM64 Neon instructions. The goal is to develop highly optimized kernels for matrix-matrix multiplication and batch-reduced matrix multiplication.
All files related to the tasks of this chapter can be found under submissions/neon/.
Execution Throughput and Latency¶
First, we will microbenchmark the execution throughput and latency of selected FP32 NEON instructions. This will provide a better understanding of their performance characteristics and serve as a reference point for performance expectations.
1. Execution Throughput¶
Task: Microbenchmark the execution throughput of the following instructions:
Each subtask is structured into four parts: the file containing the implementation of the subtask, the driver file that runs the assembly code, a compilation command to create an executable, and a short description of the results. The results of the microbenchmarks are documented in the image below:
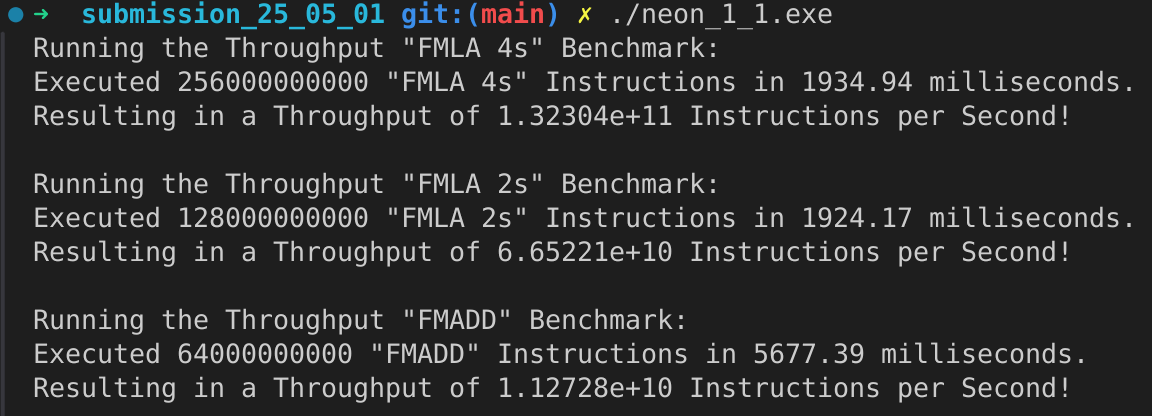
Subtask: FMLA (vector) with arrangement specifier 4S.
File:
neon_1_1.sDriver:
neon_1_1_driver.cppCompilation:
g++ -o neon_1_1.exe neon_1_1_driver.cpp neon_1_1.sWe have \(13.2304 \cdot 10^{10}\) instructions per second. That are \(132.304\) GFLOPS in total.
Subtask: FMLA (vector) with arrangement specifier 2S.
File:
neon_1_1.sDriver:
neon_1_1_driver.cppCompilation:
g++ -o neon_1_1.exe neon_1_1_driver.cpp neon_1_1.sWe have \(6.65221 \cdot 10^{10}\) instructions per second. That are \(66.5221\) GFLOPS in total.
Subtask: FMADD (scalar), single-precision variant.
File:
neon_1_1.sDriver:
neon_1_1_driver.cppCompilation:
g++ -o neon_1_1.exe neon_1_1_driver.cpp neon_1_1.sWe have \(1.12728 \cdot 10^{10}\) instructions per second. That are \(11.2728\) GFLOPS in total.
Summary
It can be seen that the usage of SIMD lanes can increase the throughput significantly. From the scala FMADD instruction to the vector
FMLA instruction with arrangement specifier 2S the throughput increases by a factor of about 6. The throughput of the vector
FMLA instruction with arrangement specifier 4S is about twice as high as the one with 2S, resulting in a factor of about 12 compared to
the scalar FMADD instruction. This shows the power of SIMD instructions and how they can be used to increase the throughput.
2. Execution Latency¶
Task: Microbenchmark the execution latency of FMLA (vector) with arrangement specifier 4s. Consider the following two cases:
Same structure as above, with the file containing the implementation of the subtask, the driver file that runs the assembly code, a compilation command to create an executable, and a short description of the results. The results of the microbenchmarks are documented in the image below:

Subtask: Dependency on one of the source registers.
File:
neon_1_2.sDriver:
neon_1_2_driver.cppCompilation:
g++ -o neon_1_2.exe neon_1_2_driver.cpp neon_1_2.sWe have \(11.4961 \cdot 10^9\) instruction per seconds in a single ALU. Resulting in a latency of \(\approx 1/3\) cycle for the known clock speed of 4.4 GHz.
Subtask: Dependency on the destination register only.
File:
neon_1_2.sDriver:
neon_1_2_driver.cppCompilation:
g++ -o neon_1_2.exe neon_1_2_driver.cpp neon_1_2.sWe have \(11.7019 \cdot 10^9\) instruction per seconds in a single ALU. Resulting in a latency of \(\approx 1/3\) cycle for the known clock speed of 4.4 GHz.
Summary
We see that the latency of the FMLA instruction is about 1/3 of a cycle, regardless of whether there is a dependency on one of the
source registers or only on the destination register.
Microkernel¶
Next, we implement the first microkernel for the matrix-matrix multiplication of \(16 \times 1\) matrices with a \(1 \times 6\) matrix which uses a \(16 \times 6\) accumulator matrix C and computes C+=AB.
1. matmul_16_6_1¶
Task: Implement a Neon microkernel that computes C+=AB for M=16, N=6, and K=1. Wrap your microkernel in the matmul_16_6_1 function.
File:
neon_2_simple.sDriver:
neon_2_driver.cpp
Implementation of the microkernel looping over each of the six columns of the matrix C:
1 ...
2 // Offset the used leading dimension by the size of floats (4byte == 2 lshifts)
3 lsl x3, x3, #2 // x3 * 4 = x3 * sizeof(float)
4 lsl x4, x4, #2 // x4 * 4 = x4 * sizeof(float)
5 lsl x5, x5, #2 // x5 * 4 = x5 * sizeof(float)
6
7 // Load all data from the 16x1 matrix a
8 ld1 {v0.4s, v1.4s, v2.4s, v3.4s}, [x0]
9
10 // Init the loop counter
11 mov x6, #6
12process_next_column:
13 // Iteration -= 1
14 subs x6, x6, #1
15
16 // Load next element from the 1x6 matrix
17 // ldr s4, [x1], #4 // one-liner but not using the argument offset
18 ldr s4, [x1]
19 add x1, x1, x4
20
21 // Load next column from the 16x6 matrix c
22 ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2]
23
24 // Calculate the next row of c
25 fmla v17.4s, v0.4s, v4.s[0]
26 fmla v18.4s, v1.4s, v4.s[0]
27 fmla v19.4s, v2.4s, v4.s[0]
28 fmla v20.4s, v3.4s, v4.s[0]
29
30 // Store the result back to memory
31 st1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
32
33 // Compare and branch on not-zero
34 cbnz x6, process_next_column
35 ...
2. Performance¶
Task: Test and optimize your microkernel. Report its performance in GFLOPS.
- Files:
neon_2.husing a loop over the columnsneon_2_unrolled.susing an unrolled version of the loop
Tests:
neon_2.test.cppBenchmarks:
neon_2.bench.cpp
Subtask: Optimization
To optimize the kernel we unrolled the loop into 3 different register ranges (v15-v28, v17-v20, v21-v24),
to allow for less dependency between the calculation of columns.
These 3 different fmla blocks gets repeated with .rept 2 to achieve the total of 6 column of calculation.
1...
2.rept 2
3// Load first element from the 1x6 matrix b
4ldr s4, [x1]
5add x1, x1, x4
6// Load first column from the 16x6 matrix c
7ld1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2]
8
9// Calculate first column of c
10fmla v25.4s, v0.4s, v4.s[0]
11fmla v26.4s, v1.4s, v4.s[0]
12fmla v27.4s, v2.4s, v4.s[0]
13fmla v28.4s, v3.4s, v4.s[0]
14
15// Store first column back to memory
16st1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
17
18// Load second element from the 1x6 matrix b
19ldr s4, [x1]
20add x1, x1, x4
21// Load second column from the 16x6 matrix c
22ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2]
23
24// Calculate second column of c
25fmla v17.4s, v0.4s, v4.s[0]
26fmla v18.4s, v1.4s, v4.s[0]
27fmla v19.4s, v2.4s, v4.s[0]
28fmla v20.4s, v3.4s, v4.s[0]
29
30// Store second column back to memory
31st1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
32
33// Load third element from the 1x6 matrix b
34ldr s4, [x1]
35add x1, x1, x4
36// Load third column from the 16x6 matrix c
37ld1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2]
38
39// Calculated third column of c
40fmla v21.4s, v0.4s, v4.s[0]
41fmla v22.4s, v1.4s, v4.s[0]
42fmla v23.4s, v2.4s, v4.s[0]
43fmla v24.4s, v3.4s, v4.s[0]
44
45// Store third column back to memory
46st1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
47.endr
48...
Subtask: Benchmarks
We run the benchmark with the following command:
./benchmarks --benchmark_counters_tabular=true --benchmark_repetitions=10 --benchmark_report_aggregates_only=true
Therefore we do 10 repetitions of the benchmark which do about 120 000 000 iterations each on our matmul kernels.
----------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
----------------------------------------------------------------------------------------------------------------------------------
Gemm16x6x1Fixture/BM_matmul_16_6_1_simple/min_warmup_time:1.000_mean 5.84 ns 5.82 ns 10 33.0036G/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_simple/min_warmup_time:1.000_median 5.83 ns 5.81 ns 10 33.0317G/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_simple/min_warmup_time:1.000_stddev 0.025 ns 0.025 ns 10 143.339M/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_simple/min_warmup_time:1.000_cv 0.43 % 0.44 % 10 0.43%
Gemm16x6x1Fixture/BM_matmul_16_6_1_unrolled/min_warmup_time:1.000_mean 5.71 ns 5.69 ns 10 33.7234G/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_unrolled/min_warmup_time:1.000_median 5.70 ns 5.68 ns 10 33.7732G/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_unrolled/min_warmup_time:1.000_stddev 0.038 ns 0.038 ns 10 224.892M/s
Gemm16x6x1Fixture/BM_matmul_16_6_1_unrolled/min_warmup_time:1.000_cv 0.67 % 0.67 % 10 0.67
We see that the simple first implementation of our matmul kernel gets about 33.0 GFLOPS. The optimized unrolled version gets about 0.7 GFLOPS more resulting in 33.7 GFLOPS.
Loops¶
To scale the microkernel to larger matrices, we will introduce loops over the K, M, and N dimensions.
1. Loop over K¶
Task: Loop over K: Implement a kernel that computes C+=AB for M=16, N=6 and K=64. Wrap your kernel in the matmul_16_6_64 function.
The first loop implemented is over the K dimension, which is the most inner loop in the matrix multiplication. The result is a microkernel that computes C+=AB for M=16, N=6 and K=64.
File
neon_3_1.s
1 ...
2 // Offset the used leading dimension by the size of floats
3 lsl x3, x3, #2 // x3 * 4 = x3 * sizeof(float)
4 lsl x4, x4, #2 // x4 * 4 = x4 * sizeof(float)
5 lsl x5, x5, #2 // x5 * 4 = x5 * sizeof(float)
6
7 mov x6, x1 // Store the initial value of x1, to be restored in the next loop iteration
8 mov x7, x2 // Store the initial value of x2, to be restored after the loop
9
10 // Load first column from the 16x6 matrix c
11 ld1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
12 // Load second column from the 16x6 matrix c
13 ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
14 // Load third column from the 16x6 matrix c
15 ld1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
16 // Load fourth column from the 16x6 matrix c
17 ld1 {v5.4s, v6.4s, v7.4s, v8.4s}, [x2], x5
18 // Load fifth column from the 16x6 matrix c
19 ld1 {v9.4s, v10.4s, v11.4s, v12.4s}, [x2], x5
20 // Load sixth column from the 16x6 matrix c
21 ld1 {v13.4s, v14.4s, v15.4s, v16.4s}, [x2], x5
22
23 mov x9, #64 // x9 iterator for K loop
24matmul_loop_over_K:
25 sub x9, x9, #1
26
27 // Load first column data from the 16x1 matrix a
28 ld1 {v0.4s, v1.4s, v2.4s, v3.4s}, [x0], x3
29
30 // run the known matmul_16_6_1_unrolled kernel
31 // Load first element from the 1x6 matrix b
32 ldr s4, [x1]
33 add x1, x1, x4
34
35 // Calculate first column of c
36 fmla v25.4s, v0.4s, v4.s[0]
37 fmla v26.4s, v1.4s, v4.s[0]
38 fmla v27.4s, v2.4s, v4.s[0]
39 fmla v28.4s, v3.4s, v4.s[0]
40
41
42 // Load second element from the 1x6 matrix b
43 ldr s4, [x1]
44 add x1, x1, x4
45
46 // Calculate second column of c
47 fmla v17.4s, v0.4s, v4.s[0]
48 fmla v18.4s, v1.4s, v4.s[0]
49 fmla v19.4s, v2.4s, v4.s[0]
50 fmla v20.4s, v3.4s, v4.s[0]
51
52
53 // Load third element from the 1x6 matrix b
54 ldr s4, [x1]
55 add x1, x1, x4
56
57 // Calculated third column of c
58 fmla v21.4s, v0.4s, v4.s[0]
59 fmla v22.4s, v1.4s, v4.s[0]
60 fmla v23.4s, v2.4s, v4.s[0]
61 fmla v24.4s, v3.4s, v4.s[0]
62
63
64 // Load fourth element from the 1x6 matrix b
65 ldr s4, [x1]
66 add x1, x1, x4
67
68 // Calculate fourth column of c
69 fmla v5.4s, v0.4s, v4.s[0]
70 fmla v6.4s, v1.4s, v4.s[0]
71 fmla v7.4s, v2.4s, v4.s[0]
72 fmla v8.4s, v3.4s, v4.s[0]
73
74
75 // Load fifth element from the 1x6 matrix b
76 ldr s4, [x1]
77 add x1, x1, x4
78
79 // Calculate fifth column of c
80 fmla v9.4s, v0.4s, v4.s[0]
81 fmla v10.4s, v1.4s, v4.s[0]
82 fmla v11.4s, v2.4s, v4.s[0]
83 fmla v12.4s, v3.4s, v4.s[0]
84
85
86 // Load sixth element from the 1x6 matrix b
87 ldr s4, [x1]
88 add x1, x1, x4
89
90 // Calculated sixth column of c
91 fmla v13.4s, v0.4s, v4.s[0]
92 fmla v14.4s, v1.4s, v4.s[0]
93 fmla v15.4s, v2.4s, v4.s[0]
94 fmla v16.4s, v3.4s, v4.s[0]
95
96
97 // offset x6 to the next element in the column
98 add x6, x6, #4 // #4 = sizeof(float)
99
100 // Restore x1 to be incremented again
101 mov x1, x6
102
103 // Loop back
104 cbnz x9, matmul_loop_over_K
105
106 // Restore initial value of x2 that was changed by the loads
107 mov x2, x7
108
109 // Store first column back to memory
110 st1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
111 // Store second column back to memory
112 st1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
113 // Store third column back to memory
114 st1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
115 // Store fourth column back to memory
116 st1 {v5.4s, v6.4s, v7.4s, v8.4s}, [x2], x5
117 // Store fifth column back to memory
118 st1 {v9.4s, v10.4s, v11.4s, v12.4s}, [x2], x5
119 // Store sixth column back to memory
120 st1 {v13.4s, v14.4s, v15.4s, v16.4s}, [x2], x5
2. Loop over M¶
Task: Loop over M: Implement a kernel that computes C+=AB for M=64, N=6 and K=64. Wrap your kernel in the matmul_64_6_64 function.
The next extension is to loop over the M dimension to allow computation of C+=AB for M=64, N=6 and K=64.
File
neon_3_2.s
1 // Offset the used leading dimension by the size of floats
2 lsl x3, x3, #2 // x3 * 4 = x3 * sizeof(float)
3 lsl x4, x4, #2 // x4 * 4 = x4 * sizeof(float)
4 lsl x5, x5, #2 // x5 * 4 = x5 * sizeof(float)
5
6 mov x6, x1 // Store the initial value of x1, to be restored in the K loop iteration
7 mov x7, x2 // Store the initial value of x2, to be restored in the K loop iteration
8
9 mov x8, x0 // Store the initial value of x0, to be restored in the M loop iteration
10 mov x9, x1 // Store the initial value of x1, to be restored in the M loop iteration
11
12 mov x16, #4 // x16 iterator for M loop
13matmul_loop_over_M:
14 sub x16, x16, #1
15
16 // ... <logic of loop over K - neon_3_1>
17
18 // next M iteration on the matrix c and matrix a, both need offset about 16 values
19 // also matrix b needs to start at the initial location again
20 // Updates for the matrix c
21 add x7, x7, #16*4 // column height * sizeof(float)
22 mov x2, x7 // also apply offset to x2
23
24 // Updates for the matrix a
25 add x8, x8, #16*4 // column height * sizeof(float)
26 mov x0, x8 // also apply offset to x0
27
28 // Updates for the matrix b
29 mov x6, x9 // Update the restore register for x1 for the K loop
30 mov x1, x9 // Update the x1 register itself
31
32 // Loop back to M
33 cbnz x16, matmul_loop_over_M
3. Loop over N¶
Task: Loop over N: Implement a kernel that computes C+=AB for M=64, N=48 and K=64. Wrap your kernel in the matmul_64_48_64 function.
The final extension is to loop over the N dimension to allow computation of C+=AB for M=64, N=48 and K=64.
File
neon_3_3.s
1 // Offset the used leading dimension by the size of floats
2 lsl x3, x3, #2 // x3 * 4 = x3 * sizeof(float)
3 lsl x4, x4, #2 // x4 * 4 = x4 * sizeof(float)
4 lsl x5, x5, #2 // x5 * 4 = x5 * sizeof(float)
5
6 mov x6, x1 // Store the initial value of x1, to be restored in the K loop iteration
7 mov x7, x2 // Store the initial value of x2, to be restored in the K loop iteration
8
9 mov x8, x0 // Store the initial value of x0, to be restored in the M loop iteration
10 mov x9, x1 // Store the initial value of x1, to be restored in the M loop iteration
11
12 mov x10, x0 // Store the initial value of x0, to be restored in the N loop iteration
13 mov x11, x2 // Store the initial value of x2, to bes restored in the N loop iteration
14 mov x12, #6 // hold the size of N that are processed in one loop, needed for offset calculation
15
16 mov x17, #8 // x17 iterator for N loop
17matmul_loop_over_N:
18 sub x17, x17, #1
19
20 // ... <logic of loop over M - neon_3_2>
21
22 // next M iteration on the matrix b and matrix c, both need offset about 6*ldb/ldc values
23 // also matrix a needs to start at the initial location again
24 // Update for the matrix a
25 mov x8, x10 // Update the restore register for x0 for the M loop
26 mov x0, x10 // Update the x0 register itself
27
28 // Updates for the matrix b
29 madd x9, x4, x12, x9 // ldb * 6 + initial position
30 mov x6, x9 // Update the restore register of x1 for the K loop
31 mov x1, x9 // Update the x1 register itself
32
33 // Updates for the matrix c
34 madd x11, x5, x12, x11 // ldc * 6 + initial position
35 mov x7, x11 // Update the restore register of x2 for the K loop
36 mov x2, x11 // Update the x2 register itself
37
38 // Loop back to N
39 cbnz x17, matmul_loop_over_N
4. Performance¶
Task: Test and optimize the kernels. Report your performance in GFLOPS.
File
neon_3.hTests
neon_3.test.cppBenchmarks
neon_3.bench.cpp
Subtask: Optimization
Usage of already optimized matmul_16_6_1 from task 2. Performance to as inner microkernel for the loop over K, M, and N.
Subtask: Benchmarks
We run the benchmark with the following command:
./benchmarks --benchmark_counters_tabular=true --benchmark_repetitions=10 --benchmark_report_aggregates_only=true
----------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
----------------------------------------------------------------------------------------------------------------------------------
GemmMxNxKFixture<16, 6, 64>/BM_matmul_16_6_64/min_warmup_time:1.000_mean 97.8 ns 97.4 ns 10 126.12G/s
GemmMxNxKFixture<16, 6, 64>/BM_matmul_16_6_64/min_warmup_time:1.000_median 97.7 ns 97.3 ns 10 126.245G/s
GemmMxNxKFixture<16, 6, 64>/BM_matmul_16_6_64/min_warmup_time:1.000_stddev 0.581 ns 0.563 ns 10 720.109M/s
GemmMxNxKFixture<16, 6, 64>/BM_matmul_16_6_64/min_warmup_time:1.000_cv 0.59 % 0.58 % 10 0.57%
GemmMxNxKFixture<64, 6, 64>/BM_matmul_64_6_64/min_warmup_time:1.000_mean 386 ns 385 ns 10 127.812G/s
GemmMxNxKFixture<64, 6, 64>/BM_matmul_64_6_64/min_warmup_time:1.000_median 385 ns 384 ns 10 127.95G/s
GemmMxNxKFixture<64, 6, 64>/BM_matmul_64_6_64/min_warmup_time:1.000_stddev 2.16 ns 2.11 ns 10 693.069M/s
GemmMxNxKFixture<64, 6, 64>/BM_matmul_64_6_64/min_warmup_time:1.000_cv 0.56 % 0.55 % 10 0.54%
GemmMxNxKFixture<64, 48, 64>/BM_matmul_64_48_64/min_warmup_time:1.000_mean 3103 ns 3092 ns 10 95.3736G/s
GemmMxNxKFixture<64, 48, 64>/BM_matmul_64_48_64/min_warmup_time:1.000_median 3097 ns 3087 ns 10 95.5363G/s
GemmMxNxKFixture<64, 48, 64>/BM_matmul_64_48_64/min_warmup_time:1.000_stddev 16.0 ns 15.6 ns 10 475.851M/s
GemmMxNxKFixture<64, 48, 64>/BM_matmul_64_48_64/min_warmup_time:1.000_cv 0.52 % 0.50 % 10 0.50%
Mean FLOPS for loop over K: 126.1 GFLOPS.
Mean FLOPS for loop over M: 127.8 GFLOPS.
Mean FLOPS for loop over N: 95.4 GFLOPS.
SIMD Lanes¶
Up to this point, our M and K dimensions have always been multiples of 4. This allowed us to fully utilize all SIMD lanes when loading and storing data from memory. That means we could load or store 4 floats at once using a single instruction, which reduces complexity and improves the performance of our kernels.
However, this assumption doesn’t always exist in real-world applications. To make our implementation more robust, we need to adapt our kernels to handle cases where the M and K dimensions are not multiples of 4. Therefore Neon supports loading 4, 2, or 1 float(s) at a time, which enables us to manage these edge cases.
1. matmul_14_6_64¶
Task: Implement a kernel that computes C+=AB for M=14, N=6 and K=64. Wrap your kernel in the matmul_14_6_64 function.
We first have a look at the case where we have a M dimension of 14. Data management can be done by loading/storing three columns of 4 floats and one column of 2 floats.
File: neon_4_1.s
For this kernel matmul_14_6_64 we adapt the already implemented kernel matmul_16_6_64. The only change is that we now use 3
ld1/st1 instructions that loads/stores on 4 scalars, and one ldr/st1 instruction that load/store the last 2 scalars: \(4 \cdot 3 + 1 \cdot 2 = 14\).
The fmla remain unchanged as we “mask” the operation by the correct load and store operations.
We load the first 14 floats and additional the last 2 floats:
1...
2// Load first column from the 14x6 matrix c - load 12 + 2 entries
3ldr d28, [x2, #12*4]
4ld1 {v25.4s, v26.4s, v27.4s}, [x2], x5
5// Load second column from the 14x6 matrix c
6ldr d20, [x2, #12*4]
7ld1 {v17.4s, v18.4s, v19.4s}, [x2], x5
8// Load third column from the 14x6 matrix c
9ldr d24, [x2, #12*4]
10ld1 {v21.4s, v22.4s, v23.4s}, [x2], x5
11// Load fourth column from the 14x6 matrix c
12ldr d8, [x2, #12*4]
13ld1 {v5.4s, v6.4s, v7.4s}, [x2], x5
14// Load fifth column from the 14x6 matrix c
15ldr d12, [x2, #12*4]
16ld1 {v9.4s, v10.4s, v11.4s}, [x2], x5
17// Load sixth column from the 14x6 matrix c
18ldr d16, [x2, #12*4]
19ld1 {v13.4s, v14.4s, v15.4s}, [x2], x5
20...
Next the loop over K:
1...
2 mov x9, #64 // x9 iterator for K loop
3matmul_loop_over_K:
4 sub x9, x9, #1
5
6 // Load first column data from the 14x1 matrix a (loading 2 + 12 entries)
7 ldr d3, [x0, #12*4]
8 ld1 {v0.4s, v1.4s, v2.4s}, [x0], x3
9
10 // run the known matmul_16_6_1_unrolled kernel with modification to matmult_14_6_1
11 // Load first element from the 1x6 matrix b
12 ldr s4, [x1]
13 add x1, x1, x4
14
15 // Calculate first column of c
16 fmla v25.4s, v0.4s, v4.s[0] // 4 floats
17 fmla v26.4s, v1.4s, v4.s[0] // 4 floats
18 fmla v27.4s, v2.4s, v4.s[0] // 4 floats
19 fmla v28.4s, v3.4s, v4.s[0] // 4 floats
20
21 // Load second element from the 1x6 matrix b
22 ldr s4, [x1]
23 add x1, x1, x4
24
25 // Calculate second column of c
26 fmla v17.4s, v0.4s, v4.s[0]
27 fmla v18.4s, v1.4s, v4.s[0]
28 fmla v19.4s, v2.4s, v4.s[0]
29 fmla v20.4s, v3.4s, v4.s[0]
30...
To store the matrix c back to memory, we use the exact same code we used to load the matrix c, but replace the load with store instructions.
1...
2// Store first column from the 14x6 matrix c - store 12 + 2 entries
3str d28, [x2, #12*4]
4st1 {v25.4s, v26.4s, v27.4s}, [x2], x5
5// Store second column from the 14x6 matrix c
6str d20, [x2, #12*4]
7st1 {v17.4s, v18.4s, v19.4s}, [x2], x5
8// Store third column from the 14x6 matrix c
9str d24, [x2, #12*4]
10st1 {v21.4s, v22.4s, v23.4s}, [x2], x5
11// Store fourth column from the 14x6 matrix c
12str d8, [x2, #12*4]
13st1 {v5.4s, v6.4s, v7.4s}, [x2], x5
14// Store fifth column from the 14x6 matrix c
15str d12, [x2, #12*4]
16st1 {v9.4s, v10.4s, v11.4s}, [x2], x5
17// Store sixth column from the 14x6 matrix c
18str d16, [x2, #12*4]
19st1 {v13.4s, v14.4s, v15.4s}, [x2], x5
20...
2. matmul_15_6_64¶
Task: Implement a kernel that computes C+=AB for M=15, N=6 and K=64. Wrap your kernel in the matmul_15_6_64 function.
The second edge case we manage is the case where we have a M dimension of 15. Data management can be done by loading/storing three columns of 4 floats, one column of 2 floats, and one time 1 float.
File: neon_4_2.s
For this kernel matmul_15_6_64 we adapt the already implemented kernel matmul_16_6_64. Similar to matmul_14_6_64 we load/store
the first 12 float and handel the last 3 elements separately. For the last 3 float we divide into a load/store of 2 elements + load/store of
1 element. Again we “mask” the computation by the load and store operation.
We load the loads 12 + 2 + 1 floats:
1...
2// Load first column from the 15x6 matrix c - load 12 + 2 + 1 entries
3ldr d28, [x2, #12*4]!
4add x2, x2, #2*4 // offset 2 elements
5ld1 {v28.s}[2],[x2]
6sub x2, x2, #14*4 // revert offset 2+12 elements
7ld1 {v25.4s, v26.4s, v27.4s}, [x2], x5
8// Load second column from the 14x6 matrix c
9ldr d20, [x2, #12*4]!
10add x2, x2, #2*4 // offset 2 elements
11ld1 {v20.s}[2],[x2]
12sub x2, x2, #14*4 // revert offset 2+12 elements
13ld1 {v17.4s, v18.4s, v19.4s}, [x2], x5
14// Load third column from the 14x6 matrix c
15ldr d24, [x2, #12*4]!
16add x2, x2, #2*4 // offset 2 elements
17ld1 {v24.s}[2],[x2]
18sub x2, x2, #14*4 // revert offset 2+12 elements
19ld1 {v21.4s, v22.4s, v23.4s}, [x2], x5
20// Load fourth column from the 14x6 matrix c
21ldr d8, [x2, #12*4]!
22add x2, x2, #2*4 // offset 2 elements
23ld1 {v8.s}[2],[x2]
24sub x2, x2, #14*4 // revert offset 2+12 elements
25ld1 {v5.4s, v6.4s, v7.4s}, [x2], x5
26// Load fifth column from the 14x6 matrix c
27ldr d12, [x2, #12*4]!
28add x2, x2, #2*4 // offset 2 elements
29ld1 {v12.s}[2],[x2]
30sub x2, x2, #14*4 // revert offset 2+12 elements
31ld1 {v9.4s, v10.4s, v11.4s}, [x2], x5
32// Load sixth column from the 14x6 matrix c
33ldr d16, [x2, #12*4]!
34add x2, x2, #2*4 // offset 2 elements
35ld1 {v16.s}[2],[x2]
36sub x2, x2, #14*4 // revert offset 2+12 elements
37ld1 {v13.4s, v14.4s, v15.4s}, [x2], x5
38...
Next the loop over K:
1...
2 mov x9, #64 // x9 iterator for K loop
3matmul_loop_over_K:
4 sub x9, x9, #1
5
6 // Load first column data from the 15x1 matrix a
7 ldr d3, [x0, #12*4]!
8 add x0, x0, #2*4 // offset 2 elements
9 ld1 {v3.s}[2],[x0]
10 sub x0, x0, #14*4 // revert offset 2+12 elements
11 ld1 {v0.4s, v1.4s, v2.4s}, [x0], x3
12
13 // run the known matmul_16_6_1_unrolled kernel with modification to matmul_15_6_1
14 // Load first element from the 1x6 matrix b
15 ldr s4, [x1]
16 add x1, x1, x4
17
18 // Calculate first column of c
19 fmla v25.4s, v0.4s, v4.s[0]
20 fmla v26.4s, v1.4s, v4.s[0]
21 fmla v27.4s, v2.4s, v4.s[0]
22 fmla v28.4s, v3.4s, v4.s[0]
23
24 // Load second element from the 1x6 matrix b
25 ldr s4, [x1]
26 add x1, x1, x4
27
28 // Calculate second column of c
29 fmla v17.4s, v0.4s, v4.s[0]
30 fmla v18.4s, v1.4s, v4.s[0]
31 fmla v19.4s, v2.4s, v4.s[0]
32 fmla v20.4s, v3.4s, v4.s[0]
33...
To store the matrix c back to memory, we use the exact same code we used to load the matrix c, but replace the load with store instructions.
1...
2// Load first column from the 15x6 matrix c - load 12 + 2 + 1 entries
3str d28, [x2, #12*4]!
4add x2, x2, #2*4 // offset 2 elements
5st1 {v28.s}[2],[x2]
6sub x2, x2, #14*4 // revert offset 2+12 elements
7st1 {v25.4s, v26.4s, v27.4s}, [x2], x5
8// Load second column from the 14x6 matrix c
9str d20, [x2, #12*4]!
10add x2, x2, #2*4 // offset 2 elements
11st1 {v20.s}[2],[x2]
12sub x2, x2, #14*4 // revert offset 2+12 elements
13st1 {v17.4s, v18.4s, v19.4s}, [x2], x5
14// Load third column from the 14x6 matrix c
15str d24, [x2, #12*4]!
16add x2, x2, #2*4 // offset 2 elements
17st1 {v24.s}[2],[x2]
18sub x2, x2, #14*4 // revert offset 2+12 elements
19st1 {v21.4s, v22.4s, v23.4s}, [x2], x5
20// Load fourth column from the 14x6 matrix c
21str d8, [x2, #12*4]!
22add x2, x2, #2*4 // offset 2 elements
23st1 {v8.s}[2],[x2]
24sub x2, x2, #14*4 // revert offset 2+12 elements
25st1 {v5.4s, v6.4s, v7.4s}, [x2], x5
26// Load fifth column from the 14x6 matrix c
27str d12, [x2, #12*4]!
28add x2, x2, #2*4 // offset 2 elements
29st1 {v12.s}[2],[x2]
30sub x2, x2, #14*4 // revert offset 2+12 elements
31st1 {v9.4s, v10.4s, v11.4s}, [x2], x5
32// Load sixth column from the 14x6 matrix c
33str d16, [x2, #12*4]!
34add x2, x2, #2*4 // offset 2 elements
35st1 {v16.s}[2],[x2]
36sub x2, x2, #14*4 // revert offset 2+12 elements
37st1 {v13.4s, v14.4s, v15.4s}, [x2], x5
38...
3. Performance¶
Task: Test and optimize the kernels. Report your performance in GFLOPS.
Since we already optimized the base kernel matmul_16_6_1 in task 2. Performance, we do not found any further
optimizations for the kernels matmul_14_6_64 and matmul_15_6_64.
Optimized benchmark results:
#TODO rerun benchmark
-----------------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
-----------------------------------------------------------------------------------------------------------------------------------------------
GemmMxNxKFixture<14, 6, 64>/BM_matmul_14_6_64/min_warmup_time:1.000_mean 98.0 ns 97.7 ns 10 110.099G/s
GemmMxNxKFixture<14, 6, 64>/BM_matmul_14_6_64/min_warmup_time:1.000_median 98.0 ns 97.7 ns 10 110.107G/s
GemmMxNxKFixture<14, 6, 64>/BM_matmul_14_6_64/min_warmup_time:1.000_stddev 0.119 ns 0.118 ns 10 132.517M/s
GemmMxNxKFixture<14, 6, 64>/BM_matmul_14_6_64/min_warmup_time:1.000_cv 0.12 % 0.12 % 10 0.12%
GemmMxNxKFixture<15, 6, 64>/BM_matmul_15_6_64/min_warmup_time:1.000_mean 104 ns 104 ns 10 110.801G/s
GemmMxNxKFixture<15, 6, 64>/BM_matmul_15_6_64/min_warmup_time:1.000_median 104 ns 104 ns 10 110.857G/s
GemmMxNxKFixture<15, 6, 64>/BM_matmul_15_6_64/min_warmup_time:1.000_stddev 0.267 ns 0.266 ns 10 283.469M/s
GemmMxNxKFixture<15, 6, 64>/BM_matmul_15_6_64/min_warmup_time:1.000_cv 0.26 % 0.26 % 10 0.26%
matmul_14_6_64 kernel: \(113.8\) GFLOPS
matmul_15_6_64 kernel: \(121.1\) GFLOPS
Accumulator Shapes¶
This section considers a matrix-matrix multiplication where a high-performance implementation may require accumulator blocks with different shapes.
1. matmul_64_64_64¶
Task: Implement a kernel that computes C+=AB for M=64, N=64 and K=64. Wrap your kernel in the matmul_64_64_64 function.
File: neon_5_1.s
For this kernel matmul_64_64_64 we adapt the already implemented kernel matmul_64_48_64. The only changes is that we removed
two fmla blocks from the inner loop i.e. our microkernel becomes a matmul_16_4_1 matrix multiplication.
1...
2 mov x15, #64 // x15 iterator for K loop
3matmul_loop_over_K:
4 sub x15, x15, #1
5
6 // Load first column data from the 16x1 matrix a
7 ld1 {v0.4s, v1.4s, v2.4s, v3.4s}, [x0], x3
8
9 // run the matmul_16_4_1_unrolled kernel
10 // Load first element from the 1x4 matrix b
11 ldr s4, [x1]
12 add x1, x1, x4
13
14 // Calculate first column of c
15 fmla v25.4s, v0.4s, v4.s[0]
16 fmla v26.4s, v1.4s, v4.s[0]
17 fmla v27.4s, v2.4s, v4.s[0]
18 fmla v28.4s, v3.4s, v4.s[0]
19
20
21 // Load second element from the 1x4 matrix b
22 ldr s4, [x1]
23 add x1, x1, x4
24
25 // Calculate second column of c
26 fmla v17.4s, v0.4s, v4.s[0]
27 fmla v18.4s, v1.4s, v4.s[0]
28 fmla v19.4s, v2.4s, v4.s[0]
29 fmla v20.4s, v3.4s, v4.s[0]
30
31
32 // Load third element from the 1x4 matrix b
33 ldr s4, [x1]
34 add x1, x1, x4
35
36 // Calculated third column of c
37 fmla v21.4s, v0.4s, v4.s[0]
38 fmla v22.4s, v1.4s, v4.s[0]
39 fmla v23.4s, v2.4s, v4.s[0]
40 fmla v24.4s, v3.4s, v4.s[0]
41
42
43 // Load fourth element from the 1x4 matrix b
44 ldr s4, [x1]
45 add x1, x1, x4
46
47 // Calculate fourth column of c
48 fmla v5.4s, v0.4s, v4.s[0]
49 fmla v6.4s, v1.4s, v4.s[0]
50 fmla v7.4s, v2.4s, v4.s[0]
51 fmla v8.4s, v3.4s, v4.s[0]
52
53
54 // offset x6 to the next element in the column
55 add x6, x6, #4 // #4 = sizeof(float)
56
57 // Restore x1 to be incremented again
58 mov x1, x6
59
60 // Loop back to K
61 cbnz x15, matmul_loop_over_K
62...
Then changed the number of loops over M to four to achieve \(4 \cdot 16 = 64\):
1...
2 mov x16, #4 // x16 iterator for M loop
3matmul_loop_over_M:
4 sub x16, x16, #1
5
6 // Load first column from the 16x4 matrix c
7 ld1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
8 // Load second column from the 16x4 matrix c
9 ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
10 // Load third column from the 16x4 matrix c
11 ld1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
12 // Load fourth column from the 16x4 matrix c
13 ld1 {v5.4s, v6.4s, v7.4s, v8.4s}, [x2], x5
14
15 mov x15, #64 // x15 iterator for K loop
16matmul_loop_over_K:
17 sub x15, x15, #1
18...
And finally changed the number of loops over N to 16 \(16 \cdot 4 = 64\):
1...
2 mov x17, #16 // x17 iterator for N loop
3matmul_loop_over_N:
4 sub x17, x17, #1
5
6 mov x16, #4 // x16 iterator for M loop
7matmul_loop_over_M:
8 sub x16, x16, #1
9...
2. Performance¶
Task: Test and optimize the kernel. Report your performance in GFLOPS.
After experimenting with different loop orders, we stay with the current order of loops over N, M, and K. The benchmark results are listed below.
--------------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
--------------------------------------------------------------------------------------------------------------------------------------------
GemmMxNxKFixture<64, 64, 64>/BM_matmul_64_64_64/min_warmup_time:1.000_mean 4111 ns 4097 ns 10 127.964G/s
GemmMxNxKFixture<64, 64, 64>/BM_matmul_64_64_64/min_warmup_time:1.000_median 4110 ns 4096 ns 10 127.988G/s
GemmMxNxKFixture<64, 64, 64>/BM_matmul_64_64_64/min_warmup_time:1.000_stddev 13.7 ns 13.8 ns 10 431.794M/s
GemmMxNxKFixture<64, 64, 64>/BM_matmul_64_64_64/min_warmup_time:1.000_cv 0.33 % 0.34 % 10 0.34%
matmul_64_64_64 kernel: \(128.0\) GFLOPS
Batch-Reduce GEMM¶
This section examines a batch-reduced matrix-matrix multiplication that introduces a fourth dimension C alongside the known M, N, and K dimensions. A batch-reduced matrix-matrix multiplication (BRGEMM or BRMM) is an operation where multiple pairs of matrices are multiplied, and their results are accumulated into a single output matrix. This operation is commonly used in machine learning to efficiently perform repeated matrix multiplications with summation across a batch dimension.
1. matmul_64_48_64_16¶
Task: Implement a kernel that computes C+=∑AᵢBᵢ for M=64, N=48 and K=64 and a batch-reduce dimension size of 16. Wrap your kernel
in the matmul_64_48_64_16 function.
File:
neon_6_1.s
We started by using our matmul_64_48_64 from 3. Loop over N kernel and replaced the microkernel with the matmul_16_4_1 as
it achieves higher performance, resulting in the file neon_6_1_no_batch.s.
1...
2 mov x17, #12 // x17 iterator for N loop
3matmul_loop_over_N:
4 sub x17, x17, #1
5
6 ...
7
8 mov x16, #4 // x16 iterator for M loop
9matmul_loop_over_M:
10 sub x16, x16, #1
11
12 ...
13
14 mov x15, #64 // x15 iterator for K loop
15matmul_loop_over_K:
16 sub x15, x15, #1
17
18 ... matmul_16_4_1 kernel ...
19
20 // Loop back to K
21 cbnz x15, matmul_loop_over_K
22
23 ...
24
25 // Loop back to M
26 cbnz x16, matmul_loop_over_M
27
28 ...
29
30 // Loop back to N
31 cbnz x17, matmul_loop_over_N
Then we wrapped the matmul_64_48_64 kernel inside another loop of size 16, representing the batch dimension:
1...
2 mov x19, #16 // x19 iterator for the batch dimension
3matmul_loop_batch_dimension:
4 sub x19, x19, #1
5
6 ...
7
8 mov x17, #12 // x17 iterator for N loop
9matmul_loop_over_N:
10 sub x17, x17, #1
11
12 ...
13
14 mov x16, #4 // x16 iterator for M loop
15matmul_loop_over_M:
16 sub x16, x16, #1
17
18 ...
19
20 mov x15, #64 // x15 iterator for K loop
21matmul_loop_over_K:
22 sub x15, x15, #1
23
24 ...
25
26 // Loop back to K
27 cbnz x15, matmul_loop_over_K
28
29 ... matmul_16_4_1 kernel ...
30
31 // Loop back to M
32 cbnz x16, matmul_loop_over_M
33
34 ...
35
36 // Loop back to N
37 cbnz x17, matmul_loop_over_N
38
39 ...
40
41 // Loop back to batch dimension
42 cbnz x19, matmul_loop_batch_dimension
2. Performance¶
Task: Test and optimize the kernel. Report your performance in GFLOPS.
We tested a variation in which the batch loop was positioned between the M and K loops. This approach achieved around \(73\) GFLOPS. We suspect that the reason for this was that the matrices did not fit into the cache. Therefore, we do not follow this approach due to the poor performance.
However, this leads us to assume that our result of putting the batch loop outside is a good choice. The benchmark results are listed below.
-----------------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
-----------------------------------------------------------------------------------------------------------------------------------------------
GemmMxNxKxBatchFixture<64, 48, 64, 1>/BM_matmul_64_48_64/min_warmup_time:1.000_mean 3104 ns 3093 ns 10 127.138G/s
GemmMxNxKxBatchFixture<64, 48, 64, 1>/BM_matmul_64_48_64/min_warmup_time:1.000_median 3102 ns 3092 ns 10 127.19G/s
GemmMxNxKxBatchFixture<64, 48, 64, 1>/BM_matmul_64_48_64/min_warmup_time:1.000_stddev 10.1 ns 8.08 ns 10 331.319M/s
GemmMxNxKxBatchFixture<64, 48, 64, 1>/BM_matmul_64_48_64/min_warmup_time:1.000_cv 0.33 % 0.26 % 10 0.26%
GemmMxNxKxBatchFixture<64, 48, 64, 16>/BM_matmul_64_48_64_16/min_warmup_time:1.000_mean 51072 ns 50890 ns 10 123.628G/s
GemmMxNxKxBatchFixture<64, 48, 64, 16>/BM_matmul_64_48_64_16/min_warmup_time:1.000_median 51027 ns 50840 ns 10 123.749G/s
GemmMxNxKxBatchFixture<64, 48, 64, 16>/BM_matmul_64_48_64_16/min_warmup_time:1.000_stddev 120 ns 119 ns 10 287.993M/s
GemmMxNxKxBatchFixture<64, 48, 64, 16>/BM_matmul_64_48_64_16/min_warmup_time:1.000_cv 0.24 % 0.23 % 10 0.23%
matmul_64_48_64 kernel: \(127.1\) GFLOPS
matmul_64_48_64_16 kernel: \(123.6\) GFLOPS
Transposition¶
The final topic of this chapter covers matrix transposition. Transposing a matrix means swapping its rows and columns which is a common operation in many matrix computations. We developed a kernel that performs the identity operation on the elements of an \(8 \times 8\) matrix stored in column-major format matrix A and writes the result in row-major format to matrix B.
1. Transpose¶
Task: Implement a Neon kernel that transposes an 8x8 matrix: B:=Aᵀ.
File: neon_7_1.s
From the lecture, we already know the \(4 \times 4\) transpose kernel. Therefore, we have the following idea:
Divide the 8x8 matrix A into four 4x4 sub-matrices
Transpose each 4x4 sub-matrix
Save T(A) and T(D) sub-matrix to matrix B
Swap sub-matrix B and C: Save T(B) to bottom-left sub-matrix of B and T(C) to top-right sub-matrix of B

Code:
1...
2/*
3* Part 1:
4* Load 4x4 sub-matrix A.
5* Transpose 4x4 block.
6* Store 4x4 block of A into B.
7*/
8// Load
9ldr q0, [x4]
10add x4, x4, x2
11ldr q1, [x4]
12add x4, x4, x2
13ldr q2, [x4]
14add x4, x4, x2
15ldr q3, [x4]
16
17// Transpose
18trn1 v4.4s, v0.4s, v1.4s
19trn2 v5.4s, v0.4s, v1.4s
20trn1 v6.4s, v2.4s, v3.4s
21trn2 v7.4s, v2.4s, v3.4s
22
23zip1 v8.2d, v4.2d, v6.2d
24zip1 v9.2d, v5.2d, v7.2d
25zip2 v10.2d, v4.2d, v6.2d
26zip2 v11.2d, v5.2d, v7.2d
27
28// Store
29str q8, [x5]
30add x5, x5, x3
31str q9, [x5]
32add x5, x5, x3
33str q10, [x5]
34add x5, x5, x3
35str q11, [x5]
36
37/*
38* Part 2:
39* Load 4x4 sub-matrix B and C.
40* Transpose both 4x4 blocks.
41* Store both 4x4 blocks of C and B into B.
42*/
43// Load right-top
44mov x4, x0 // A
45add x4, x4, #128 // Offset to top-left corner of right half of A (32th element)
46...
47
48// Transpose right-top
49...
50
51// Load left-bottom
52mov x4, x0 // A
53add x4, x4, #16 // Offset to next 4 elements of column in A (4th element)
54...
55
56// Transpose left-bottom
57...
58
59// Store after transpose to avoid conflicts when input matrix A = B
60// Store B to C (right-top of A to left-bottom of B)
61mov x5, x1
62add x5, x5, #16
63...
64
65// Store C to B (left-bottom of A to right-top of B)
66mov x5, x1
67add x5, x5, #128
68...
69
70/*
71* Part 3:
72* Load 4x4 sub-matrix D.
73* Transpose 4x4 block.
74* Store 4x4 block of A into B.
75*/
76// Load
77mov x4, x0 // A
78add x4, x4, #144 // 128 + 16 -> left-top corner of right-bottom 4x4 sub-matrix of A
79...
80
81// Transpose
82...
83
84// Store
85mov x5, x1 // A
86add x5, x5, #144 // 128 + 16 -> left-top corner of right-bottom 4x4 sub-matrix of B
87...
2. Performance¶
Task: Test and optimize your kernel. Report its performance in GiB/s.
We benchmarked the performance of our transpose kernel and achieved the following results:
--------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Byte
--------------------------------------------------------------------------------------------------------------
Trans8x8Fixture/BT_tran_8_8/min_warmup_time:1.000_mean 5.08 ns 5.06 ns 10 101.188G/s
Trans8x8Fixture/BT_tran_8_8/min_warmup_time:1.000_median 5.07 ns 5.06 ns 10 101.277G/s
Trans8x8Fixture/BT_tran_8_8/min_warmup_time:1.000_stddev 0.030 ns 0.030 ns 10 590.962M/s
Trans8x8Fixture/BT_tran_8_8/min_warmup_time:1.000_cv 0.59 % 0.59 % 10 0.58%
trans_8_8 kernel: \(101.2\) GiB/s