Code Generation¶
This chapter introduces the code generation of the kernels developed in Neon chapter supporting Aarch64 instructions. We will take a look at a wrapper of the Aarch64 instructions to generate 32 bit instructions during the runtime that will than be used to compose the kernels.
The general workflow of generating JITed code is: 1. Generate the kernel. 2. Write the kernel to a new memory page. 3. Make the memory page executable & flush the instruction cache to load the page. 4. Use the pointer to the memory page as a function pointer to execute the JITed kernel.
src/main/arm_instructions/ directory.src/main/kernels/ directory.src/main/.Note
The equivalent tests for files can be found in the src/test/ directory with the same name extended by .test.
BRGEMM Primitive¶
First, we will develop software that generates batch-reduce matrix-matrix multiplications (BRGEMMs) i.e. \(C\ \)\(+\)\(=\)\(\ \sum_i A_i \cdot B_i\).
- Files:
Brgemm.cppKernel.cpp
Microkernel¶
In this section we take first steps of code generation by wrapping the Aarch64 instructions and writing the first matmul_16_6_1 kernel
with variable k loop size.
1. Generate¶
Task: Start implementing the generate function. Support only the single setting of an FP32 Neon microkernel that computes C+=AB for
column-major matrices and M=16, N=6, and K=1. Return an appropriate error code if the parameters of the function differ from this setting.
The generate function will be used to compose the correct matrix multiplication kernel to a given set of parameters: Dimension size of
M, N, K, Batch, column- or row-major format of matrices A, B, C, and data type.
At runtime we can then call the generated kernel and propagate the pointer to the A, B, C matrices along with their respective leading dimension and the batch stride of the A and B matrices.
To compose our kernel we need to write the correct Aarch64 instructions as 32 bit representation i.e. uin32_t to a consecutive memory space.
To write the instructions in a more assembly like manner we wrapped each required instruction into a function.
Thus, each instruction we generate has a wrapper which is based on the following structure:
First asserts are placed to check if the instruction is used correctly to evade most errors from misusage.
The instruction is build using masking operation and shifts to the starting bit of the opcode “block”.
For example the post variant of the load instructions with an immediate (LDR (immediate)):
1constexpr uint32_t ldrImmediatePost(const uint32_t Rt, const uint32_t Rn, const int32_t imm9, const bool is64bit)
2{
3 release_assert(((Rt & mask5) == Rt), "Rt is only allowed to have a size of 5 bit.");
4 release_assert(((Rn & mask5) == Rn), "Rn is only allowed to have a size of 5 bit.");
5 release_assert(imm9 <= 255, "imm9 has a Maximum of 255");
6 release_assert(imm9 >= -256, "imm9 has a Minimum of -256");
7
8 uint32_t ldr = 0;
9 ldr |= 0b1 << 31; // size bit 31
10 ldr |= (is64bit & mask1) << 30;
11 ldr |= 0b111000010 << 21; // opc 29 - 21
12 ldr |= (imm9 & mask9) << 12;
13 ldr |= 0b01 << 10; // opc 11 - 10
14 ldr |= (Rn & mask5) << 5;
15 ldr |= (Rt & mask5) << 0;
16 return ldr;
17}
This function then gets wrapped to match the definition of our enum class for each register.
1constexpr uint32_t ldrPost(const R32Bit Wt, const R64Bit Xn, const int32_t imm9)
2{
3 return internal::ldrImmediatePost(static_cast<uint32_t>(Wt), static_cast<uint32_t>(Xn), imm9, false);
4}
5
6constexpr uint32_t ldrPost(const R64Bit Xt, const R64Bit Xn, const int32_t imm9)
7{
8 return internal::ldrImmediatePost(static_cast<uint32_t>(Xt), static_cast<uint32_t>(Xn), imm9, true);
9}
Note
All these function have the keyword constexpr at the start. This has the benefit that most processing of the instruction can be done at compile time. Such that we get the following assembly code is produces:
All inputs are fixed, it compiles into 2 mov instructions
mov w1, #38073 // =0x94b9 movk w1, #63557, lsl #16
On input is known at runtime, it compiles into 3 instructions
mov w1, #38048 // =0x94a0 movk w1, #63557, lsl #16 bfxil x1, x8, #0, #5
Thus we do speedup the creation of the code generation, as most inputs are known at compile time.
After writing a lot wrappers around the arm instructions.
We can translate our previous assembly kernel using c++ function and generate the matmul_16_6_1 at runtime.
1void mini_jit::kernels::matmul_16_6_1(mini_jit::Kernel &kernel)
2{
3 using namespace mini_jit::arm_instructions;
4
5 kernel.add({
6 // Offset the used leading dimension by the size of floats
7 lsl(x3, x3, 2), // lsl x3, x3, #2
8 lsl(x4, x4, 2), // lsl x4, x4, #2
9 lsl(x5, x5, 2), // lsl x5, x5, #2
10
11 // Load all data from the 16x1 matrix a
12 ld1(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x0) // ld1 {v0.4s, v1.4s, v2.4s, v3.4s}, [x0]
13 });
14
15 for (int i = 0; i < 2; i++)
16 {
17 kernel.add({
18 // Load first element from the 1x6 matrix b
19 ldr(s4, x1), // ldr s4, [x1] WARNING
20 add(x1, x1, x4), // add x1, x1, x4
21 // Load first column from the 16x6 matrix c
22 ld1(v25, t4s, v26, t4s, v27, t4s, v28, t4s, x2), // ld1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2]
23
24 // Calculate first column of c
25 fmla(v25, t4s, v0, t4s, v4, 0), // fmla v25.4s, v0.4s, v4.s[0]
26 fmla(v26, t4s, v1, t4s, v4, 0), // fmla v26.4s, v1.4s, v4.s[0]
27 fmla(v27, t4s, v2, t4s, v4, 0), // fmla v27.4s, v2.4s, v4.s[0]
28 fmla(v28, t4s, v3, t4s, v4, 0), // fmla v28.4s, v3.4s, v4.s[0]
29
30 // Store first column back to memory
31 st1Post(v25, t4s, v26, t4s, v27, t4s, v28, t4s, x2, x5), // st1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
32
33 // Load second element from the 1x6 matrix b
34 ldr(s4, x1), // ldr s4, [x1]
35 add(x1, x1, x4), // add x1, x1, x4
36 // Load second column from the 16x6 matrix c
37 ld1(v17, t4s, v18, t4s, v19, t4s, v20, t4s, x2), // ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2]
38
39 // Calculate second column of c
40 fmla(v17, t4s, v0, t4s, v4, 0), // fmla v17.4s, v0.4s, v4.s[0]
41 fmla(v18, t4s, v1, t4s, v4, 0), // fmla v18.4s, v1.4s, v4.s[0]
42 fmla(v19, t4s, v2, t4s, v4, 0), // fmla v19.4s, v2.4s, v4.s[0]
43 fmla(v20, t4s, v3, t4s, v4, 0), // fmla v20.4s, v3.4s, v4.s[0]
44
45 // Store second column back to memory
46 st1Post(v17, t4s, v18, t4s, v19, t4s, v20, t4s, x2, x5), // st1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
47
48 // Load third element from the 1x6 matrix b
49 ldr(s4, x1), // ldr s4, [x1]
50 add(x1, x1, x4), // add x1, x1, x4
51 // Load third column from the 16x6 matrix c
52 ld1(v21, t4s, v22, t4s, v23, t4s, v24, t4s, x2), // ld1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2]
53
54 // Calculated third column of c
55 fmla(v21, t4s, v0, t4s, v4, 0), // fmla v21.4s, v0.4s, v4.s[0]
56 fmla(v22, t4s, v1, t4s, v4, 0), // fmla v22.4s, v1.4s, v4.s[0]
57 fmla(v23, t4s, v2, t4s, v4, 0), // fmla v23.4s, v2.4s, v4.s[0]
58 fmla(v24, t4s, v3, t4s, v4, 0), // fmla v24.4s, v3.4s, v4.s[0]
59
60 // Store third column back to memory
61 st1Post(v21, t4s, v22, t4s, v23, t4s, v24, t4s, x2, x5), // st1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
62 });
63 }
64
65 kernel.add(ret()); // ret
66
67 kernel.write("matmul_16_6_1.bin");
68}
In the original assembly we used .rept 2.
We can replicate that using a simple for loop.
Note
The kernel has two add functions. One for adding an uint32_t and one to add a vector<uint32_t>.
To reduce writing overhead of kernel.add.
2. k parameter support¶
Task: Add support for the k parameter by generating a K loop around the microkernel.
Adding support for the k parameter does require adding more wrapped instructions.
But then we can port our assembly kernel to c++ and jit the k loop parameter.
1void mini_jit::kernels::matmul_16_6_k(mini_jit::Kernel &kernel, const uint32_t k_loop)
2{
3 using namespace mini_jit::arm_instructions;
4
5 // Procedural Call Standard
6 // save frame pointer and link register
7 kernel.add({
8
9 stpPre(fp, lr, sp, -16), // stp fp, lr, [sp, #-16]!
10 // update frame pointer to current stack pointer
11 movSp(fp, sp), // mov fp, sp
12
13 // save callee-saved registers
14 stpPre(x19, x20, sp, -16), // stp x19, x20, [sp, #-16]!
15 stpPre(x21, x22, sp, -16), // stp x21, x22, [sp, #-16]!
16 stpPre(x23, x24, sp, -16), // stp x23, x24, [sp, #-16]!
17 stpPre(x25, x26, sp, -16), // stp x25, x26, [sp, #-16]!
18 stpPre(x27, x28, sp, -16), // stp x27, x28, [sp, #-16]!
19
20 stpPre(d8, d9, sp, -16), // stp d8, d9, [sp, #-16]!
21 stpPre(d10, d11, sp, -16), // stp d10, d11, [sp, #-16]!
22 stpPre(d12, d13, sp, -16), // stp d12, d13, [sp, #-16]!
23 stpPre(d14, d15, sp, -16), // stp d14, d15, [sp, #-16]!
24
25 // Offset the used leading dimension by the size of floats
26 lsl(x3, x3, 2), // lsl x3, x3, #2
27 lsl(x4, x4, 2), // lsl x4, x4, #2
28 lsl(x5, x5, 2), // lsl x5, x5, #2
29
30 mov(x6, x1), // mov x6, x1
31 mov(x7, x2), // mov x7, x2
32
33 // Load first column from the 16x6 matrix c
34 ld1Post(v25, t4s, v26, t4s, v27, t4s, v28, t4s, x2, x5), // ld1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
35 // Load second column from the 16x6 matrix c
36 ld1Post(v17, t4s, v18, t4s, v19, t4s, v20, t4s, x2, x5), // ld1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
37 // Load third column from the 16x6 matrix c
38 ld1Post(v21, t4s, v22, t4s, v23, t4s, v24, t4s, x2, x5), // ld1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
39 // Load fourth column from the 16x6 matrix c
40 ld1Post(v5, t4s, v6, t4s, v7, t4s, v8, t4s, x2, x5), // ld1 {v5.4s, v6.4s, v7.4s, v8.4s}, [x2], x5
41 // Load fifth column from the 16x6 matrix c
42 ld1Post(v9, t4s, v10, t4s, v11, t4s, v12, t4s, x2, x5), // ld1 {v9.4s, v10.4s, v11.4s, v12.4s}, [x2], x5
43 // Load sixth column from the 16x6 matrix c
44 ld1Post(v13, t4s, v14, t4s, v15, t4s, v16, t4s, x2, x5), // ld1 {v13.4s, v14.4s, v15.4s, v16.4s}, [x2], x5
45
46 movz(x9, k_loop), // mov x9, "iterator for K loop"
47
48 // #############################
49 // #### matmul_loop_over_K: ####
50 // #############################
51 sub(x9, x9, 1), // sub x9, x9, #1
52
53 // Load first column data from the 16x1 matrix a
54 ld1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x0, x3), // ld1 {v0.4s, v1.4s, v2.4s, v3.4s}, [x0], x3
55
56 // run the known matmul_16_6_1_unrolled kernel
57 // Load first element from the 1x6 matrix b
58 ldr(s4, x1), // ldr s4, [x1]
59 add(x1, x1, x4), // add x1, x1, x4
60
61 // Calculate first column of c
62 fmla(v25, t4s, v0, t4s, v4, 0), // fmla v25.4s, v0.4s, v4.s[0]
63 fmla(v26, t4s, v1, t4s, v4, 0), // fmla v26.4s, v1.4s, v4.s[0]
64 fmla(v27, t4s, v2, t4s, v4, 0), // fmla v27.4s, v2.4s, v4.s[0]
65 fmla(v28, t4s, v3, t4s, v4, 0), // fmla v28.4s, v3.4s, v4.s[0]
66
67
68 // Load second element from the 1x6 matrix b
69 ldr(s4, x1), // ldr s4, [x1]
70 add(x1, x1, x4), // add x1, x1, x4
71
72 // Calculate second column of c
73 fmla(v17, t4s, v0, t4s, v4, 0), // fmla v17.4s, v0.4s, v4.s[0]
74 fmla(v18, t4s, v1, t4s, v4, 0), // fmla v18.4s, v1.4s, v4.s[0]
75 fmla(v19, t4s, v2, t4s, v4, 0), // fmla v19.4s, v2.4s, v4.s[0]
76 fmla(v20, t4s, v3, t4s, v4, 0), // fmla v20.4s, v3.4s, v4.s[0]
77
78
79 // Load third element from the 1x6 matrix b
80 ldr(s4, x1), // ldr s4, [x1]
81 add(x1, x1, x4), // add x1, x1, x4
82
83 // Calculated third column of c
84 fmla(v21, t4s, v0, t4s, v4, 0), // fmla v21.4s, v0.4s, v4.s[0]
85 fmla(v22, t4s, v1, t4s, v4, 0), // fmla v22.4s, v1.4s, v4.s[0]
86 fmla(v23, t4s, v2, t4s, v4, 0), // fmla v23.4s, v2.4s, v4.s[0]
87 fmla(v24, t4s, v3, t4s, v4, 0), // fmla v24.4s, v3.4s, v4.s[0]
88
89
90 // Load fourth element from the 1x6 matrix b
91 ldr(s4, x1), // ldr s4, [x1]
92 add(x1, x1, x4), // add x1, x1, x4
93
94 // Calculate fourth column of c
95 fmla(v5, t4s, v0, t4s, v4, 0), // fmla v5.4s, v0.4s, v4.s[0]
96 fmla(v6, t4s, v1, t4s, v4, 0), // fmla v6.4s, v1.4s, v4.s[0]
97 fmla(v7, t4s, v2, t4s, v4, 0), // fmla v7.4s, v2.4s, v4.s[0]
98 fmla(v8, t4s, v3, t4s, v4, 0), // fmla v8.4s, v3.4s, v4.s[0]
99
100
101 // Load fifth element from the 1x6 matrix b
102 ldr(s4, x1), // ldr s4, [x1]
103 add(x1, x1, x4), // add x1, x1, x4
104
105 // Calculate fifth column of c
106 fmla(v9, t4s, v0, t4s, v4, 0), // fmla v9.4s, v0.4s, v4.s[0]
107 fmla(v10, t4s, v1, t4s, v4, 0), // fmla v10.4s, v1.4s, v4.s[0]
108 fmla(v11, t4s, v2, t4s, v4, 0), // fmla v11.4s, v2.4s, v4.s[0]
109 fmla(v12, t4s, v3, t4s, v4, 0), // fmla v12.4s, v3.4s, v4.s[0]
110
111
112 // Load sixth element from the 1x6 matrix b
113 ldr(s4, x1), // ldr s4, [x1]
114 add(x1, x1, x4), // add x1, x1, x4
115
116 // Calculated sixth column of c
117 fmla(v13, t4s, v0, t4s, v4, 0), // fmla v13.4s, v0.4s, v4.s[0]
118 fmla(v14, t4s, v1, t4s, v4, 0), // fmla v14.4s, v1.4s, v4.s[0]
119 fmla(v15, t4s, v2, t4s, v4, 0), // fmla v15.4s, v2.4s, v4.s[0]
120 fmla(v16, t4s, v3, t4s, v4, 0), // fmla v16.4s, v3.4s, v4.s[0]
121
122
123 // offset x6 to the next element in the column
124 add(x6, x6, 4), // add x6, x6, #4 // #4 = sizeof(float)
125
126 // Restore x1 to be incremented again
127 mov(x1, x6), // mov x1, x6
128
129 // Loop back
130 cbnz(x9, -40*4), // cbnz x9, matmul_loop_over_K
131
132 // Restore initial value of x2 that was changed by the loads
133 mov(x2, x7), // mov x2, x7
134
135 // Store first column back to memory
136 st1Post(v25, t4s, v26, t4s, v27, t4s, v28, t4s, x2, x5), // st1 {v25.4s, v26.4s, v27.4s, v28.4s}, [x2], x5
137 // Store second column back to memory
138 st1Post(v17, t4s, v18, t4s, v19, t4s, v20, t4s, x2, x5), // st1 {v17.4s, v18.4s, v19.4s, v20.4s}, [x2], x5
139 // Store third column back to memory
140 st1Post(v21, t4s, v22, t4s, v23, t4s, v24, t4s, x2, x5), // st1 {v21.4s, v22.4s, v23.4s, v24.4s}, [x2], x5
141 // Store fourth column back to memory
142 st1Post(v5, t4s, v6, t4s, v7, t4s, v8, t4s, x2, x5), // st1 {v5.4s, v6.4s, v7.4s, v8.4s}, [x2], x5
143 // Store fifth column back to memory
144 st1Post(v9, t4s, v10, t4s, v11, t4s, v12, t4s, x2, x5), // st1 {v9.4s, v10.4s, v11.4s, v12.4s}, [x2], x5
145 // Store sixth column back to memory
146 st1Post(v13, t4s, v14, t4s, v15, t4s, v16, t4s, x2, x5), // st1 {v13.4s, v14.4s, v15.4s, v16.4s}, [x2], x5
147
148 // Procedural Call Standard
149 // restore callee-saved registers
150 ldpPost(d14, d15, sp, 16), // ldp d14, d15, [sp], #16
151 ldpPost(d12, d13, sp, 16), // ldp d12, d13, [sp], #16
152 ldpPost(d10, d11, sp, 16), // ldp d10, d11, [sp], #16
153 ldpPost(d8, d9, sp, 16), // ldp d8, d9, [sp], #16
154
155 ldpPost(x27, x28, sp, 16), // ldp x27, x28, [sp], #16
156 ldpPost(x25, x26, sp, 16), // ldp x25, x26, [sp], #16
157 ldpPost(x23, x24, sp, 16), // ldp x23, x24, [sp], #16
158 ldpPost(x21, x22, sp, 16), // ldp x21, x22, [sp], #16
159 ldpPost(x19, x20, sp, 16), // ldp x19, x20, [sp], #16
160
161 // restore frame pointer and link register
162 ldpPost(fp, lr, sp, 16), // ldp fp, lr, [sp], #16
163
164 ret() // ret
165 });
166
167 kernel.write("matmul_16_6_k.bin");
168}
Looking at the first highlight. This is our adjusted instruction at runtime, using the given loop count for the k dimension.
movz(x9, k_loop), // mov x9, "iterator for K loop"
Another interesting instruction, is the second highlight. We need to manually calculate the offset. Which in our case, we jump 40 instructions to loop again.
cbnz(x9, -40*4), // cbnz x9, matmul_loop_over_K
3. Performance¶
Task: Test the kernel generation. Report performance in GFLOPS.
Testing our JITed kernel, we get the same performance as out previous implementation.
Note
The generation of the matmul kernel is done outside of the benchmarking loop, as one would do in a real world scenario.
------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations FLOPS
------------------------------------------------------------------------------------------------------------------------------------
GemmJited16x6x1Fixture/BM_jited_matmul_16_6_1/min_warmup_time:1.000_mean 5.57 ns 5.56 ns 10 34.5601G/s
GemmJited16x6x1Fixture/BM_jited_matmul_16_6_1/min_warmup_time:1.000_median 5.56 ns 5.55 ns 10 34.6245G/s
GemmJited16x6x1Fixture/BM_jited_matmul_16_6_1/min_warmup_time:1.000_stddev 0.041 ns 0.040 ns 10 249.138M/s
GemmJited16x6x1Fixture/BM_jited_matmul_16_6_1/min_warmup_time:1.000_cv 0.73 % 0.72 % 10 0.72%
GemmJited16x6x128Fixture/BM_jited_matmul_16_6_128/min_warmup_time:1.000_mean 187 ns 187 ns 10 131.579G/s
GemmJited16x6x128Fixture/BM_jited_matmul_16_6_128/min_warmup_time:1.000_median 187 ns 186 ns 10 131.811G/s
GemmJited16x6x128Fixture/BM_jited_matmul_16_6_128/min_warmup_time:1.000_stddev 1.02 ns 1.01 ns 10 702.935M/s
GemmJited16x6x128Fixture/BM_jited_matmul_16_6_128/min_warmup_time:1.000_cv 0.54 % 0.54 % 10 0.53%
jited_matmul_16_6_1 kernel: \(34.6\) GFLOPS
jited_matmul_16_6_k(=128) kernel: \(131.6\) GFLOPS
GEMM¶
We will now take a look at the basic GEMM implementation i.e. C+=AB.
1. Generate¶
Task: Extend the implementation of the generate function to support all M-N-K combinations for C+=AB as specified above. Assume that all matrices are in column-major format.
To support all combinations of M, N and K, we use one kernel as a base and dynamically generate the rest of the numbers that are not multiples of M, N or K.
As a base we took the matmul_16m_4n_k kernel, which reached around 130 GFLOPS as 64_48_64 kernel.
The k dimension is always a multiple of 1, thus we don’t need a special case for this dimension.
To get full coverage on the remaining dimension, we iteratively implemented the following variations:
- matmul_16m_lt4nRest_k:
M dimension must be multiple of 16
N dimension can be less than 4 or larger, multiple of 4 are processed at once, N mod 4 are processed at the end at once
- matmul_16mRest_4n_k:
M dimension can be larger than 16, multiple of 16 are processed at once, M mod 16 are processed at the end at once
N dimension must be multiple of 4
- matmul_16mRest_lt4nRest_k:
M dimension can be larger than 16, multiple of 16 are processed at once, M mod 16 are processed at the end at once
N dimension can be less than 4 or larger, multiple of 4 are processed at once, N mod 4 are processed at the end at once
- matmul_lt16_4n_k:
M dimension must be less than 16
N dimension must be multiple of 4
- matmul_lt16_lt4nRest_k:
M dimension must be less than 16
N dimension can be less than 4 or larger, multiple of 4 are processed at once, N mod 4 are processed at the end at once
Together with the matmul_16m_4n_k, we have 6 kernels to cover the complete dimension space.
2. Verify kernel generation¶
Task: Verify your kernel generation by comparing to a reference implementation for 1≤M≤64, 1≤N≤64 and K∈[1,16,32,64,128], and by setting lda=M, ldb=K, ldc=M.
We tests all these configurations with counting upwards and random data. The tests can be found in Brgemm.test.cpp.
All test configuration habe passed.
3. Verfiy edge cases¶
Task: Verify the kernel generation in cases where lda>M, ldb>K or ldc>M.
Also for higher leading dimension we tests all these configurations with counting upwards and random data. The tests can also be found in
Brgemm.test.cpp. All test configuration habe passed.
4. Performance¶
Task: Benchmark the performance of your generated kernels and report the measured performance for 1≤M≤64, 1≤N≤64, K∈[1,16,32,64,128], lda=M, ldb=K and ldc=M. Use a CSV format for output. Follow the structure of the example file data/perf.csv. Report the arithmetic mean performance of all settings in GFLOPS.
The benchmark took approximately eight hours in total to run. The following results were produced: GEMM_benchmarks.csv
We can visualize the dataset across the three dimension m, n, k:
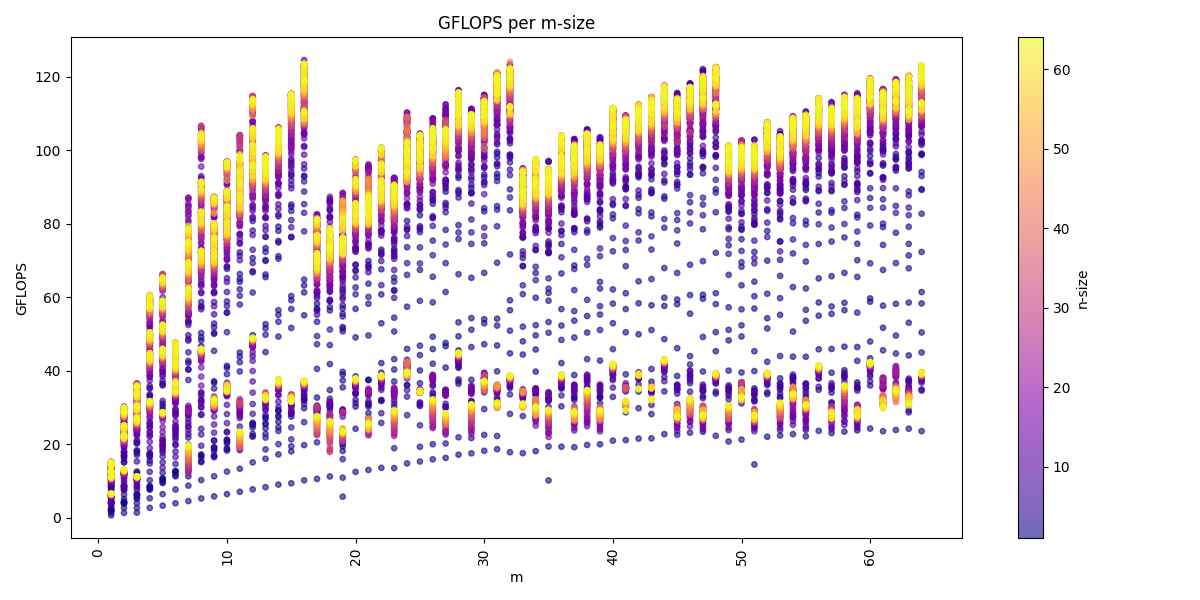
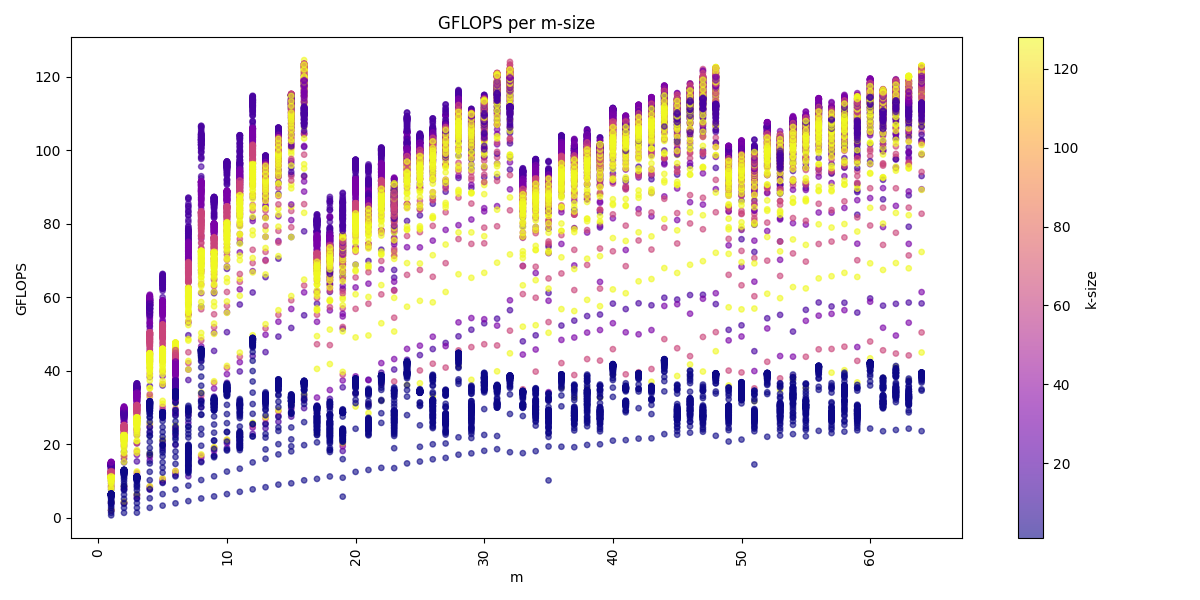
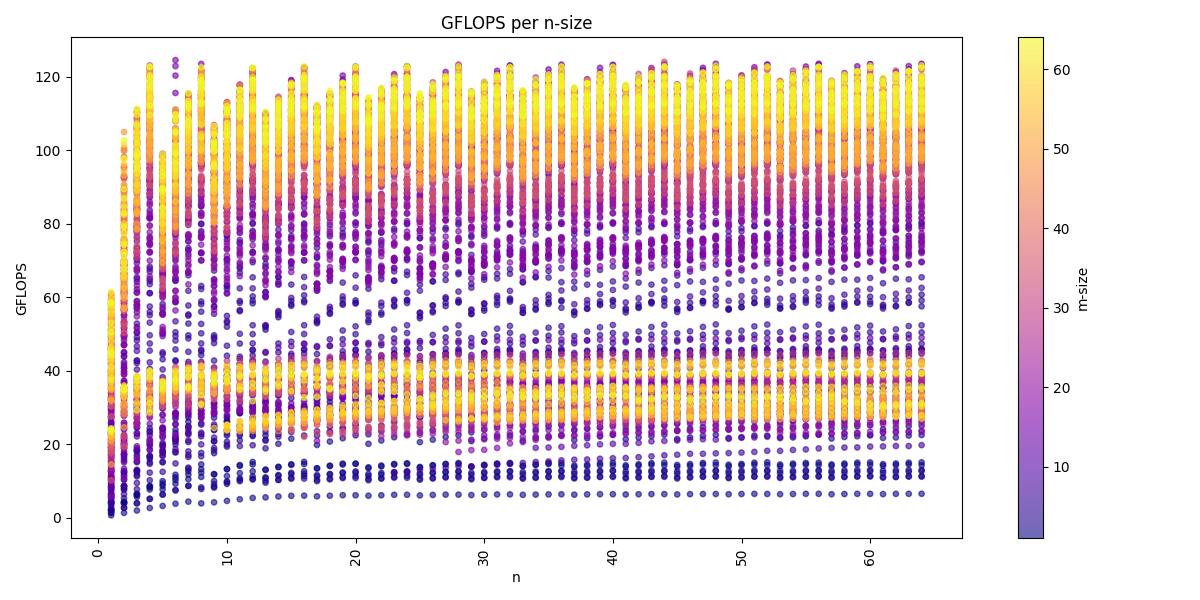
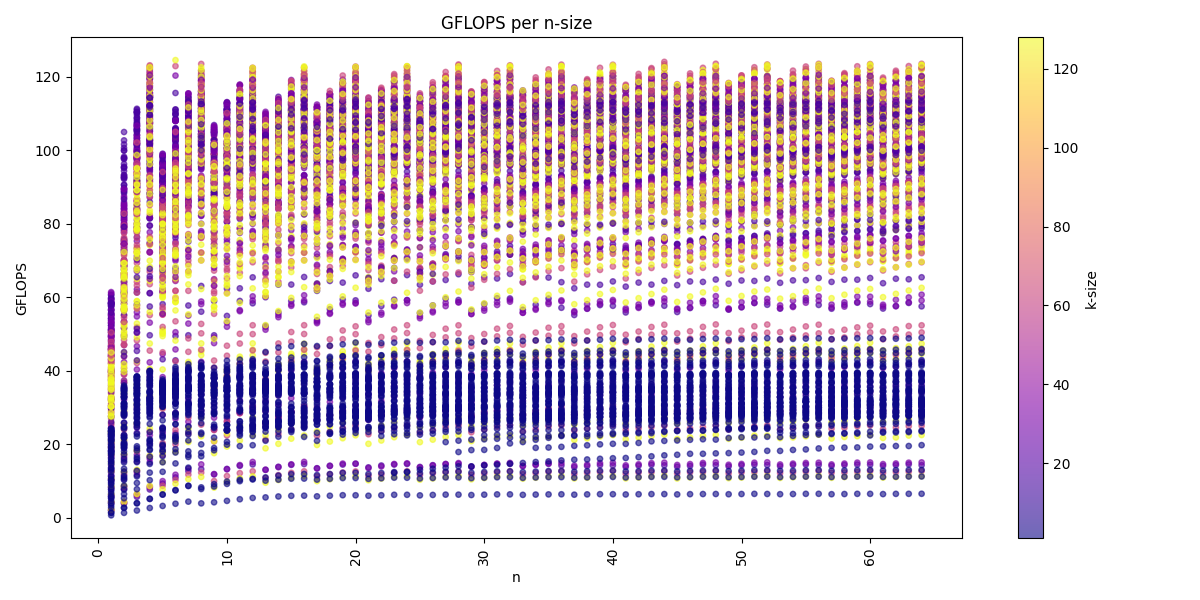
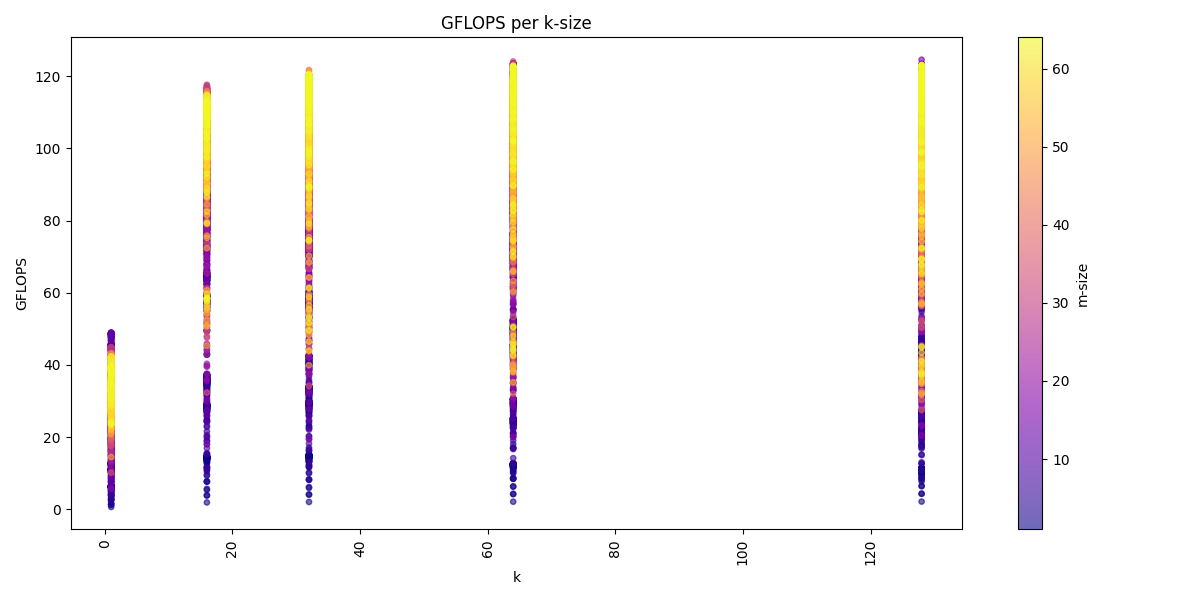
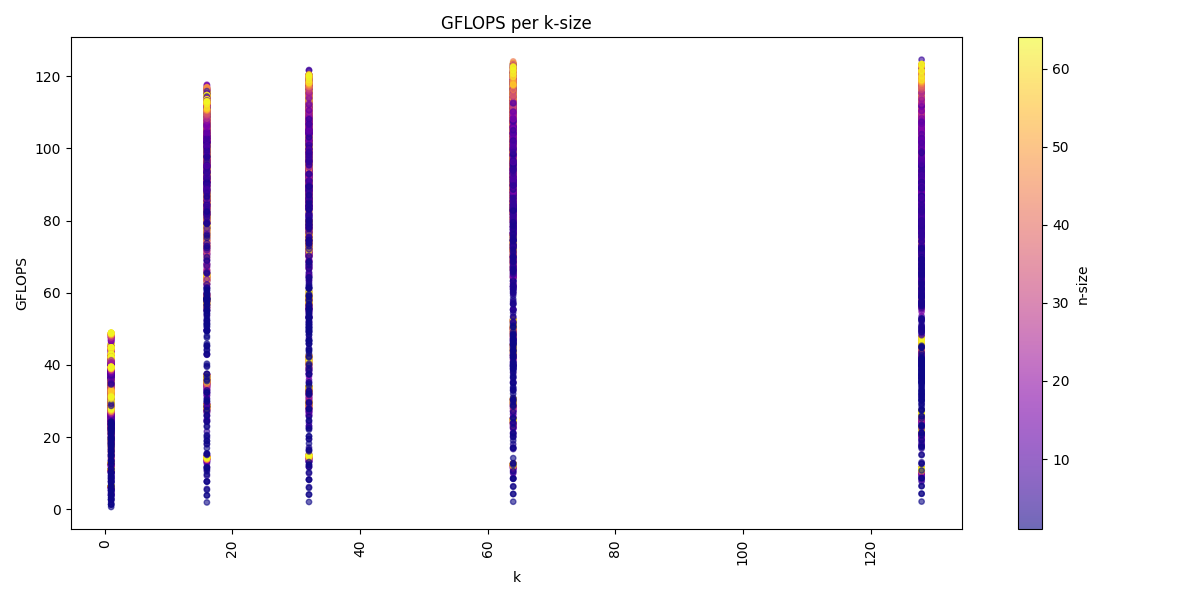
We see for the m-dimension that multiple of 16 are the best performing matrices sizes. We also see that we get usually higher performance with increasing k-dimension and also a higher n-dimension, but a higher k-dimension is more important.
The arithmetic mean of all benchmarks is: 80.1 GFLOPS
Batch-Reduce GEMM¶
Now we can extend the GEMM implementation by an additional batch-dimension i.e. C+=∑AᵢBᵢ.
1. generate¶
Task: Extend the implementation of the generate function to support batch-reduce GEMMs: C+=∑AᵢBᵢ. Assume that all matrices are in column-major format.
In order to support an additional batch dimension in our implemented kernels, we placed all kernels within an additional batch loop.
Consequently, the logic in our Brgemm.cpp was extended to check whether the batch dimension is greater than one.
1...
2if (dtype != dtype_t::fp32)
3{
4 return error_t::err_wrong_dtype;
5}
6if (m == 0 || n == 0 || k == 0)
7{
8 return error_t::err_wrong_dimension;
9}
10if ((trans_a + trans_b + trans_c) != 0)
11{
12 return error_t::err_row_major_order_not_supported;
13}
14
15if (br_size == 1 && (trans_a + trans_b + trans_c) == 0 && dtype == dtype_t::fp32)
16{
17 fill_with_matmuls_no_batch_dim_column_major_fp32(m, n, k);
18}
19else if (br_size > 1 && (trans_a + trans_b + trans_c) == 0 && dtype == dtype_t::fp32)
20{
21 fill_with_matmuls_batch_dim_column_major_fp32(m, n, k, br_size);
22}
23else
24{
25 throw std::logic_error(
26 std::format("Unhandled parameter combination found: m='{}', n='{}', k='{}', br_size='{}', trans_a='{}', trans_b='{}', "
27 "trans_c = '{}', dtype = '{}'",
28 m, n, k, br_size, trans_a, trans_b, trans_c, static_cast<int32_t>(dtype)));
29}
30...
This else if branch distributes to our extended br_matmul_* kernels with a larger batch dimension.
br_matmul_16m_lt4nRest_k
br_matmul_16mRest_4n_k
br_matmul_16mRest_lt4nRest_k
br_matmul_lt16_4n_k
br_matmul_lt16_lt4nRest_k
2. Verfiy¶
Task: Verify your generated kernels against a reference implementation.
All kernels were tested. The tests are located in the file src/test/kernels/br_matmul_*.test.cpp.
The batched MatMul generation was tested for 1≤M≤64, 1≤N≤64, K∈[1,16,32,64,128], 1≤BatchSize≤16, lda=M, ldb=K, and ldc=M.
The test is located in the file src/test/Brgemm.test.cpp.
3. Performance¶
Task: Benchmark the performance of your generated kernels and report the measured performance for 1≤M≤64, 1≤N≤64, K∈[1,16,32,64,128], br_size=16, br_stride_a=M*K, br_stride_b=K*N, lda=M, ldb=K, and ldc=M. Report the arithmetic mean performance of all settings in GFLOPS.
The benchmark took approximately eight hours in total to run. The following results were produced: GEMM_benchmarks.csv
We can visualize the dataset across the three dimension m, n, k:

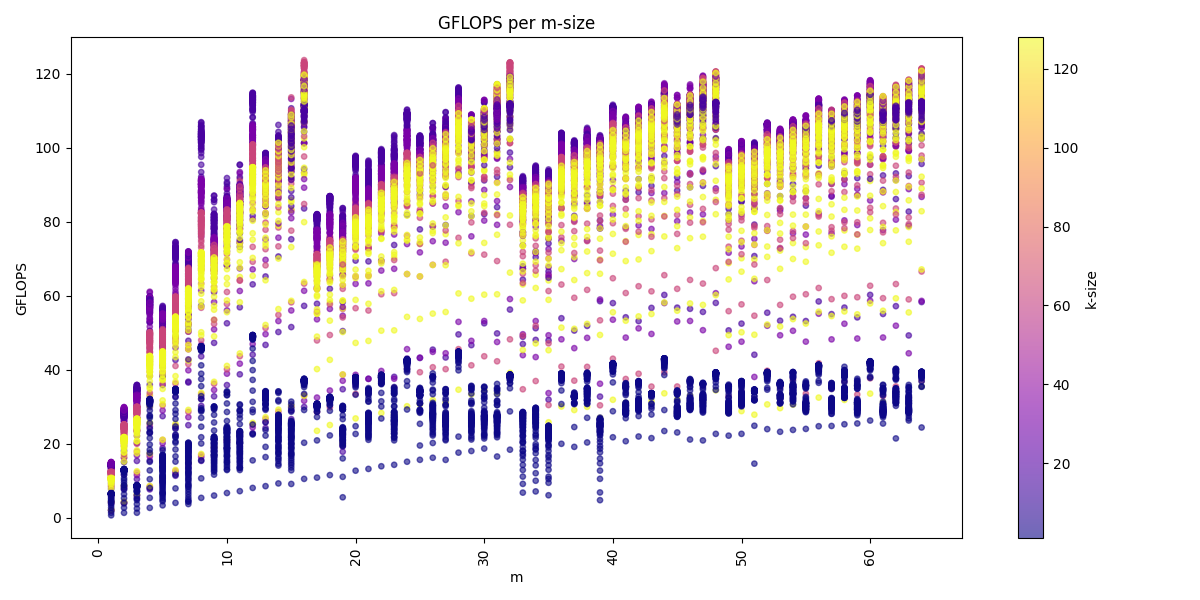
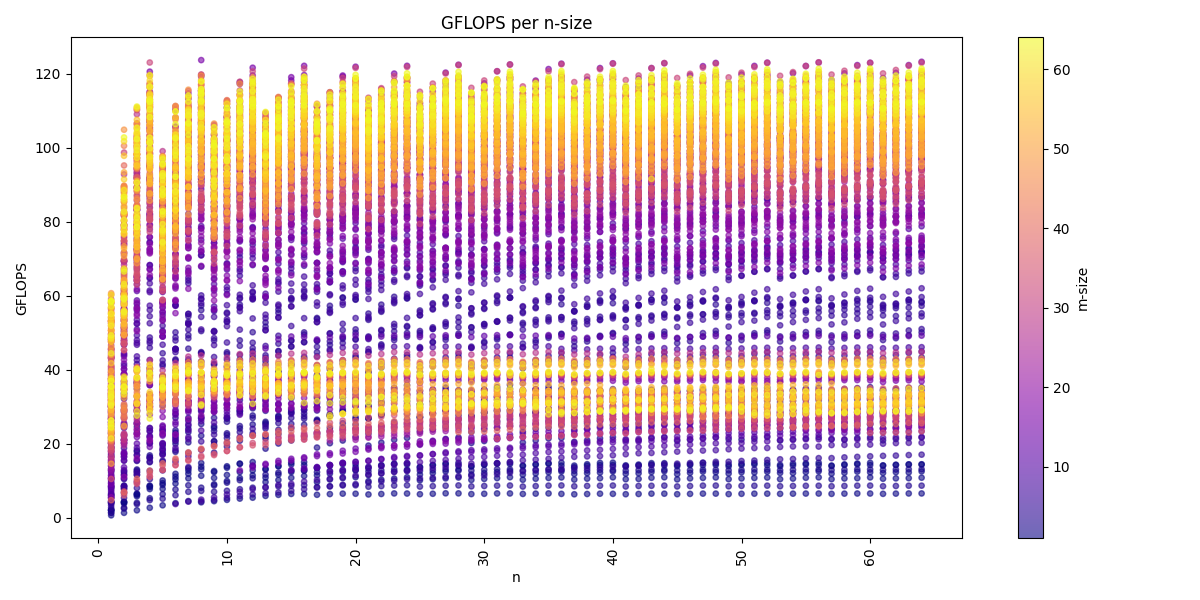
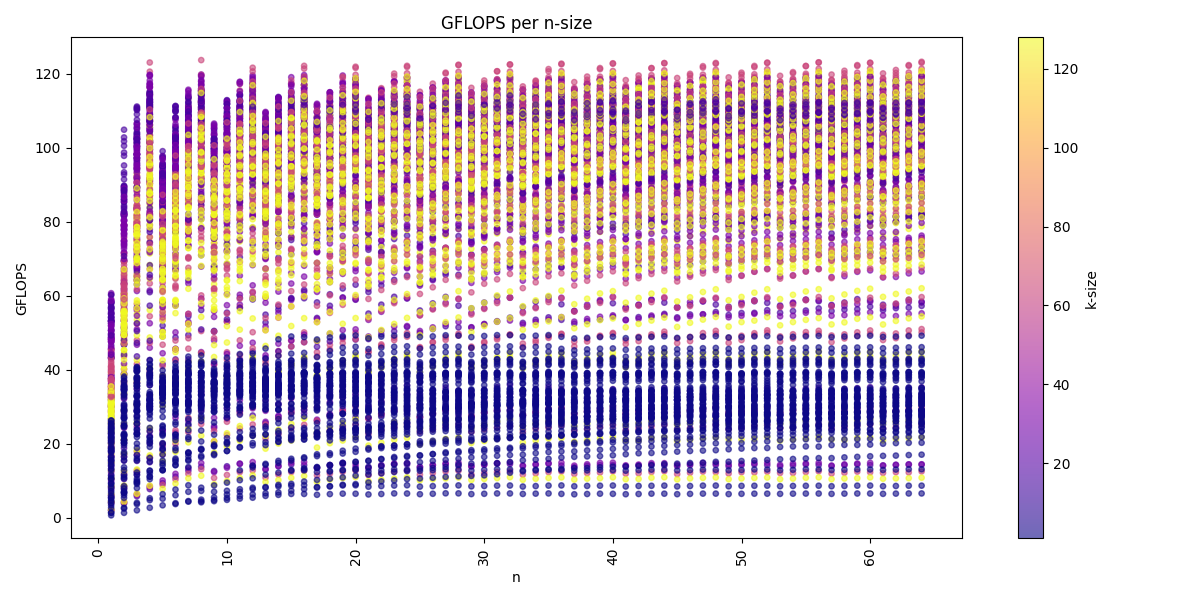
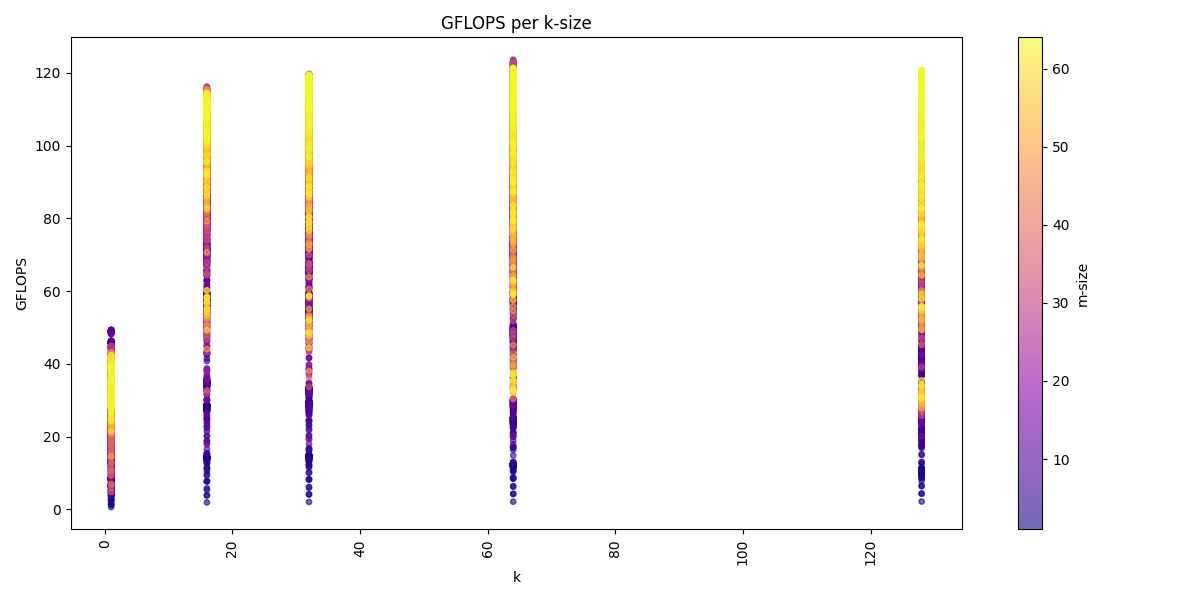
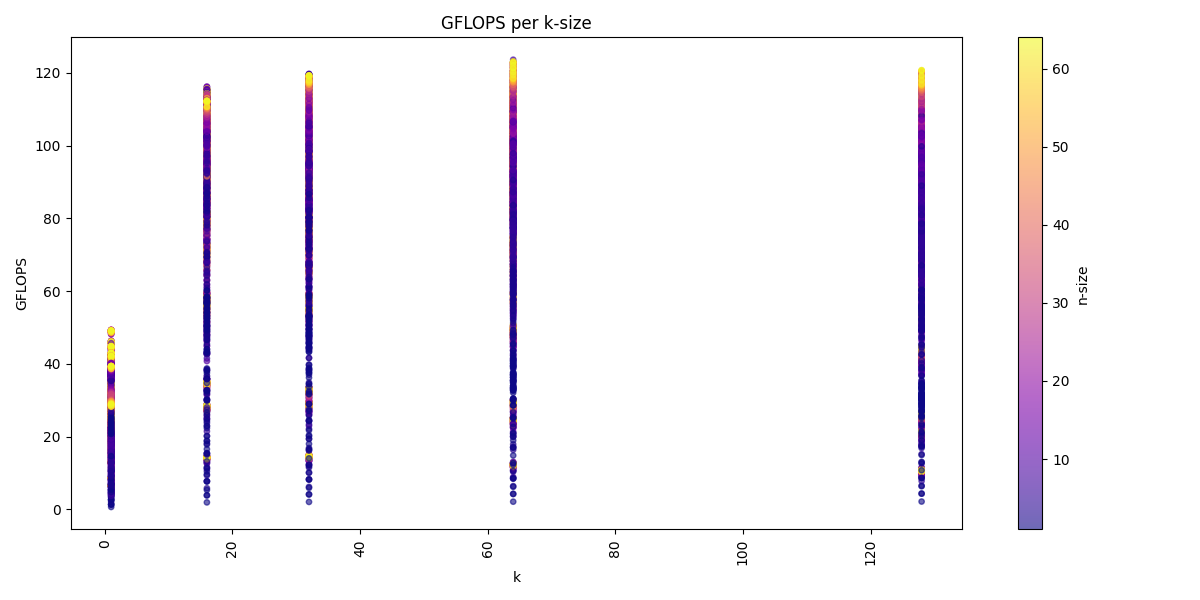
Again we see for the m-dimension that multiple of 16 are the best performing matrices sizes. We also see that we get usually higher performance with increasing k-dimension and also a higher n-dimension, but a higher k-dimension is more important. The batch-dimension does not have a noticeable impact on the performance compared to the benchmarks in the GEMM kernels.
Unary Primitives¶
Now we further extend our kernel with primitives. Primitives are operation which only operate one one input i.e. B:=op(A). We will take a look at the Zero, Identity and ReLU primitives and their transpose variants.
Zero Primitive¶
This primitives ignores the input and filles all element of the output with zeros.
1. generate¶
Task: Begin implementing the mini_jit::Unary::generate function by adding support for the zero primitive.
File: unary_zero.cpp
Again we implement a generate function
which is used to compose the correct primitive kernel to a given set of parameters: Dimension size of
M, N, column- or row-major format of matrices B, data type, and Primitive type.
At runtime we can then call the generated kernel and propagate the pointer to the A, B matrices along with their respective leading dimension.
For the zero primitive we zero four register which are then stored to the correct memory space.
Note
This kernel is again used as a base and the we generate the rest of the number not multiple of M and dynamically.
...
// Zero four register so we can fill the matrix with zeros
eor(v0, t16b, v0, t16b, v0, t16b), // Zero the v0 register
eor(v1, t16b, v1, t16b, v1, t16b), // Zero the v1 register
eor(v2, t16b, v2, t16b, v2, t16b), // Zero the v2 register
eor(v3, t16b, v3, t16b, v3, t16b), // Zero the v3 register
...
...
// x17 iterator for the m_loop
mov(x17, m_loop_16),
// loop over m
sub(x17, x17, 1),
st1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x1, x9), // increase x1 after store with value of x2 i.e. x1 += 4 * 16 Byte
// loop back to m
cbnz(x17, -2 * 4),
...
2. Performance¶
Task: Test and benchmark representative kernels. Include at least settings with M=N=50, M=N=64, M=N=512 and M=N=2048. Report performance in GiB/s.
Without Transposition
-------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Bytes
-------------------------------------------------------------------------------------------------------------------------------
UnaryFixture/BM_unary_zero/M:50/N:50/min_warmup_time:1.000_mean 97.5 ns 97.2 ns 10 205.828G/s
UnaryFixture/BM_unary_zero/M:50/N:50/min_warmup_time:1.000_median 97.3 ns 97.0 ns 10 206.267G/s
UnaryFixture/BM_unary_zero/M:50/N:50/min_warmup_time:1.000_stddev 0.983 ns 0.980 ns 10 2.05822G/s
UnaryFixture/BM_unary_zero/M:50/N:50/min_warmup_time:1.000_cv 1.01 % 1.01 % 10 1.00%
UnaryFixture/BM_unary_zero/M:64/N:64/min_warmup_time:1.000_mean 186 ns 185 ns 10 176.895G/s
UnaryFixture/BM_unary_zero/M:64/N:64/min_warmup_time:1.000_median 184 ns 183 ns 10 179.139G/s
UnaryFixture/BM_unary_zero/M:64/N:64/min_warmup_time:1.000_stddev 7.19 ns 7.16 ns 10 6.55984G/s
UnaryFixture/BM_unary_zero/M:64/N:64/min_warmup_time:1.000_cv 3.86 % 3.86 % 10 3.71%
UnaryFixture/BM_unary_zero/M:512/N:512/min_warmup_time:1.000_mean 9205 ns 9174 ns 10 228.836G/s
UnaryFixture/BM_unary_zero/M:512/N:512/min_warmup_time:1.000_median 9345 ns 9314 ns 10 225.169G/s
UnaryFixture/BM_unary_zero/M:512/N:512/min_warmup_time:1.000_stddev 316 ns 314 ns 10 7.95304G/s
UnaryFixture/BM_unary_zero/M:512/N:512/min_warmup_time:1.000_cv 3.43 % 3.43 % 10 3.48%
UnaryFixture/BM_unary_zero/M:2048/N:2048/min_warmup_time:1.000_mean 265455 ns 264356 ns 10 127.786G/s
UnaryFixture/BM_unary_zero/M:2048/N:2048/min_warmup_time:1.000_median 256886 ns 255806 ns 10 131.171G/s
UnaryFixture/BM_unary_zero/M:2048/N:2048/min_warmup_time:1.000_stddev 24366 ns 24271 ns 10 10.4142G/s
UnaryFixture/BM_unary_zero/M:2048/N:2048/min_warmup_time:1.000_cv 9.18 % 9.18 % 10 8.15%
BM_unary_zero/M:50/N:50 kernel: \(206.3\) GiB/s
BM_unary_zero/M:64/N:64 kernel: \(176.9\) GiB/s
BM_unary_zero/M:512/N:512 kernel: \(228.8\) GiB/s
BM_unary_zero/M:2048/N:2048 kernel: \(127.8\) GiB/s
With Transposition
Transposition is the equivalent operation with swapped M und N dimension. Thus we get the same performance.
Identity Primitive¶
1. generate¶
Task: Extend the implementation of the mini_jit::Unary::generate function to support the identity primitive.
Files: unary_identity.cpp & unary_identity_transpose.cpp
Similar to the zero kernel but now we read the kernel from the A matrix and store the loaded values back the the B matrix.
...
// x17 iterator for the m_loop
mov(x17, m_loop / 16),
// loop over m
sub(x17, x17, 1),
ld1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x0, x9), // increase x0 after load with value of x9 i.e. x0 += 4 * 4 * sizeof(float)
st1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x1, x9), // increase x1 after store with value of x9 i.e. x1 += 4 * 4 * sizeof(float)
// loop back to m
cbnz(x17, -3 * 4),
...
For the transpose kernel we implement a transposition on a generic matrix by transposing 4x4 blocks a storing them back to the correct positions. Similar to the idea discussed in Neon - Transpose.
For example the transpose of the 4x4 block, where we again implemented transpose for all 16 combinations of \((\le 4) \times (\le 4)\).
The function call to ops generates the correct operations on the loaded registers i.e. for the identity operation these does not append any instructions,
because we already load and store the transposed matrix.
...
kernel.add({
// // Load
ldr(q0, x4), // ldr q0, [x4]
add(x4, x4, x2), // add x4, x4, x2
ldr(q1, x4), // ldr q1, [x4]
add(x4, x4, x2), // add x4, x4, x2
ldr(q2, x4), // ldr q2, [x4]
add(x4, x4, x2), // add x4, x4, x2
ldr(q3, x4), // ldr q3, [x4]
});
ops(kernel, v0);
ops(kernel, v1);
ops(kernel, v2);
ops(kernel, v3);
kernel.add({
// // Transpose
trn1(v4, t4s, v0, t4s, v1, t4s), // trn1 v4.4s, v0.4s, v1.4s
trn2(v5, t4s, v0, t4s, v1, t4s), // trn2 v5.4s, v0.4s, v1.4s
trn1(v6, t4s, v2, t4s, v3, t4s), // trn1 v6.4s, v2.4s, v3.4s
trn2(v7, t4s, v2, t4s, v3, t4s), // trn2 v7.4s, v2.4s, v3.4s
//
zip1(v8, t2d, v4, t2d, v6, t2d), // zip1 v8.2d, v4.2d, v6.2d
zip1(v9, t2d, v5, t2d, v7, t2d), // zip1 v9.2d, v5.2d, v7.2d
zip2(v10, t2d, v4, t2d, v6, t2d), // zip2 v10.2d, v4.2d, v6.2d
zip2(v11, t2d, v5, t2d, v7, t2d), // zip2 v11.2d, v5.2d, v7.2d
// // Store
str(q8, x5), // str q8, [x5]
add(x5, x5, x3), // add x5, x5, x3
str(q9, x5), // str q9, [x5]
add(x5, x5, x3), // add x5, x5, x3
str(q10, x5), // str q10, [x5]
add(x5, x5, x3), // add x5, x5, x3
str(q11, x5), // str q11, [x5]
});
2. Performance¶
Task: Test and benchmark representative kernels. Include at least settings with M=N=50, M=N=64, M=N=512 and M=N=2048. Report performance in GiB/s.
Without Transposition
-------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Bytes
-------------------------------------------------------------------------------------------------------------------------------
UnaryFixture/BM_unary_identity/M:50/N:50/min_warmup_time:1.000_mean 129 ns 129 ns 10 155.397G/s
UnaryFixture/BM_unary_identity/M:50/N:50/min_warmup_time:1.000_median 129 ns 128 ns 10 155.951G/s
UnaryFixture/BM_unary_identity/M:50/N:50/min_warmup_time:1.000_stddev 1.53 ns 1.49 ns 10 1.7808G/s
UnaryFixture/BM_unary_identity/M:50/N:50/min_warmup_time:1.000_cv 1.18 % 1.16 % 10 1.15%
UnaryFixture/BM_unary_identity/M:64/N:64/min_warmup_time:1.000_mean 202 ns 202 ns 10 163.002G/s
UnaryFixture/BM_unary_identity/M:64/N:64/min_warmup_time:1.000_median 200 ns 200 ns 10 164.143G/s
UnaryFixture/BM_unary_identity/M:64/N:64/min_warmup_time:1.000_stddev 11.4 ns 11.3 ns 10 8.26683G/s
UnaryFixture/BM_unary_identity/M:64/N:64/min_warmup_time:1.000_cv 5.65 % 5.62 % 10 5.07%
UnaryFixture/BM_unary_identity/M:512/N:512/min_warmup_time:1.000_mean 16864 ns 16789 ns 10 125.139G/s
UnaryFixture/BM_unary_identity/M:512/N:512/min_warmup_time:1.000_median 16468 ns 16388 ns 10 127.967G/s
UnaryFixture/BM_unary_identity/M:512/N:512/min_warmup_time:1.000_stddev 776 ns 768 ns 10 5.48377G/s
UnaryFixture/BM_unary_identity/M:512/N:512/min_warmup_time:1.000_cv 4.60 % 4.57 % 10 4.38%
UnaryFixture/BM_unary_identity/M:2048/N:2048/min_warmup_time:1.000_mean 317943 ns 315684 ns 10 106.416G/s
UnaryFixture/BM_unary_identity/M:2048/N:2048/min_warmup_time:1.000_median 316519 ns 314379 ns 10 106.733G/s
UnaryFixture/BM_unary_identity/M:2048/N:2048/min_warmup_time:1.000_stddev 11615 ns 11358 ns 10 3.8664G/s
UnaryFixture/BM_unary_identity/M:2048/N:2048/min_warmup_time:1.000_cv 3.65 % 3.60 % 10 3.63%
BM_unary_identity/M:50/N:50 kernel: \(155.4\) GiB/s
BM_unary_identity/M:64/N:64 kernel: \(163.0\) GiB/s
BM_unary_identity/M:512/N:512 kernel: \(125.1\) GiB/s
BM_unary_identity/M:2048/N:2048 kernel: \(106.4\) GiB/s
With Transposition
-----------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Bytes
-----------------------------------------------------------------------------------------------------------------------------------------
UnaryFixture/BM_unary_identity_transpose/M:50/N:50/min_warmup_time:1.000_mean 157 ns 156 ns 10 128.118G/s
UnaryFixture/BM_unary_identity_transpose/M:50/N:50/min_warmup_time:1.000_median 157 ns 156 ns 10 128.093G/s
UnaryFixture/BM_unary_identity_transpose/M:50/N:50/min_warmup_time:1.000_stddev 0.734 ns 0.732 ns 10 600.086M/s
UnaryFixture/BM_unary_identity_transpose/M:50/N:50/min_warmup_time:1.000_cv 0.47 % 0.47 % 10 0.47%
UnaryFixture/BM_unary_identity_transpose/M:64/N:64/min_warmup_time:1.000_mean 252 ns 251 ns 10 130.502G/s
UnaryFixture/BM_unary_identity_transpose/M:64/N:64/min_warmup_time:1.000_median 252 ns 251 ns 10 130.41G/s
UnaryFixture/BM_unary_identity_transpose/M:64/N:64/min_warmup_time:1.000_stddev 1.12 ns 1.10 ns 10 573.58M/s
UnaryFixture/BM_unary_identity_transpose/M:64/N:64/min_warmup_time:1.000_cv 0.44 % 0.44 % 10 0.44%
UnaryFixture/BM_unary_identity_transpose/M:512/N:512/min_warmup_time:1.000_mean 477698 ns 476113 ns 10 4.40967G/s
UnaryFixture/BM_unary_identity_transpose/M:512/N:512/min_warmup_time:1.000_median 478232 ns 476633 ns 10 4.39994G/s
UnaryFixture/BM_unary_identity_transpose/M:512/N:512/min_warmup_time:1.000_stddev 16842 ns 16774 ns 10 155.727M/s
UnaryFixture/BM_unary_identity_transpose/M:512/N:512/min_warmup_time:1.000_cv 3.53 % 3.52 % 10 3.53%
UnaryFixture/BM_unary_identity_transpose/M:2048/N:2048/min_warmup_time:1.000_mean 8826949 ns 8790588 ns 10 3.81791G/s
UnaryFixture/BM_unary_identity_transpose/M:2048/N:2048/min_warmup_time:1.000_median 8813603 ns 8778155 ns 10 3.8225G/s
UnaryFixture/BM_unary_identity_transpose/M:2048/N:2048/min_warmup_time:1.000_stddev 137200 ns 136627 ns 10 59.0859M/s
UnaryFixture/BM_unary_identity_transpose/M:2048/N:2048/min_warmup_time:1.000_cv 1.55 % 1.55 % 10 1.55%
BM_unary_identity_transpose/M:50/N:50 kernel: \(128.1\) GiB/s
BM_unary_identity_transpose/M:64/N:64 kernel: \(130.5\) GiB/s
BM_unary_identity_transpose/M:512/N:512 kernel: \(4.409\) GiB/s
BM_unary_identity_transpose/M:2048/N:2048 kernel: \(3.817\) GiB/s
ReLU Primitive¶
1. generate¶
Task: Extend the implementation of the mini_jit::Unary::generate function to support the ReLU primitive.
Files: unary_relu.cpp & unary_relu_transpose.cpp
Here we do the exact same as the identity kernel in the transpose and none-transpose kernel, but with an additional hard-coded zero vector register and and additional fmax between the load and the store operation.
...
// x17 iterator for the m_loop
mov(x17, m_loop / 16),
// loop over m
sub(x17, x17, 1),
ld1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x0, x9), // increase x0 after load with value of x9 i.e. x0 += 4 * 4 * sizeof(float)
fmax(v0, t4s, v0, t4s, v5, t4s),
fmax(v1, t4s, v1, t4s, v5, t4s),
fmax(v2, t4s, v2, t4s, v5, t4s),
fmax(v3, t4s, v3, t4s, v5, t4s),
st1Post(v0, t4s, v1, t4s, v2, t4s, v3, t4s, x1, x9), // increase x1 after store with value of x9 i.e. x1 += 4 * 4 * sizeof(float)
// loop back to m
cbnz(x17, -7 * 4),
...
In addition, the ops function of the transpose kernel becomes:
void relu(mini_jit::Kernel &kernel, mini_jit::arm_instructions::VGeneral vRegister)
{
using namespace mini_jit::arm_instructions;
kernel.add(fmax(vRegister, t4s, vRegister, t4s, v31, t4s));
}
2. Performance¶
Task: Test and benchmark representative kernels. Include at least settings with M=N=50, M=N=64, M=N=512 and M=N=2048. Report performance in GiB/s.
Without Transposition
---------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Bytes
---------------------------------------------------------------------------------------------------------------------------
UnaryFixture/BM_unary_relu/M:50/N:50/min_warmup_time:1.000_mean 141 ns 140 ns 10 143.13G/s
UnaryFixture/BM_unary_relu/M:50/N:50/min_warmup_time:1.000_median 137 ns 137 ns 10 146.168G/s
UnaryFixture/BM_unary_relu/M:50/N:50/min_warmup_time:1.000_stddev 8.16 ns 8.03 ns 10 7.717G/s
UnaryFixture/BM_unary_relu/M:50/N:50/min_warmup_time:1.000_cv 5.80 % 5.73 % 10 5.39%
UnaryFixture/BM_unary_relu/M:64/N:64/min_warmup_time:1.000_mean 223 ns 222 ns 10 147.933G/s
UnaryFixture/BM_unary_relu/M:64/N:64/min_warmup_time:1.000_median 221 ns 220 ns 10 148.866G/s
UnaryFixture/BM_unary_relu/M:64/N:64/min_warmup_time:1.000_stddev 14.6 ns 14.4 ns 10 9.37165G/s
UnaryFixture/BM_unary_relu/M:64/N:64/min_warmup_time:1.000_cv 6.56 % 6.49 % 10 6.34%
UnaryFixture/BM_unary_relu/M:512/N:512/min_warmup_time:1.000_mean 16615 ns 16550 ns 10 126.752G/s
UnaryFixture/BM_unary_relu/M:512/N:512/min_warmup_time:1.000_median 16695 ns 16624 ns 10 126.155G/s
UnaryFixture/BM_unary_relu/M:512/N:512/min_warmup_time:1.000_stddev 281 ns 281 ns 10 2.24229G/s
UnaryFixture/BM_unary_relu/M:512/N:512/min_warmup_time:1.000_cv 1.69 % 1.70 % 10 1.77%
UnaryFixture/BM_unary_relu/M:2048/N:2048/min_warmup_time:1.000_mean 314145 ns 312183 ns 10 107.534G/s
UnaryFixture/BM_unary_relu/M:2048/N:2048/min_warmup_time:1.000_median 316017 ns 313907 ns 10 106.899G/s
UnaryFixture/BM_unary_relu/M:2048/N:2048/min_warmup_time:1.000_stddev 7378 ns 7145 ns 10 2.48532G/s
UnaryFixture/BM_unary_relu/M:2048/N:2048/min_warmup_time:1.000_cv 2.35 % 2.29 % 10 2.31%
BM_unary_relu/M:50/N:50 kernel: \(143.1\) GiB/s
BM_unary_relu/M:64/N:64 kernel: \(148.0\) GiB/s
BM_unary_relu/M:512/N:512 kernel: \(126.8\) GiB/s
BM_unary_relu/M:2048/N:2048 kernel: \(107.5\) GiB/s
With Transposition
-------------------------------------------------------------------------------------------------------------------------------------
Benchmark Time CPU Iterations Bytes
-------------------------------------------------------------------------------------------------------------------------------------
UnaryFixture/BM_unary_relu_transpose/M:50/N:50/min_warmup_time:1.000_mean 159 ns 158 ns 10 126.468G/s
UnaryFixture/BM_unary_relu_transpose/M:50/N:50/min_warmup_time:1.000_median 159 ns 158 ns 10 126.509G/s
UnaryFixture/BM_unary_relu_transpose/M:50/N:50/min_warmup_time:1.000_stddev 0.839 ns 0.826 ns 10 660.394M/s
UnaryFixture/BM_unary_relu_transpose/M:50/N:50/min_warmup_time:1.000_cv 0.53 % 0.52 % 10 0.52%
UnaryFixture/BM_unary_relu_transpose/M:64/N:64/min_warmup_time:1.000_mean 244 ns 243 ns 10 134.75G/s
UnaryFixture/BM_unary_relu_transpose/M:64/N:64/min_warmup_time:1.000_median 244 ns 243 ns 10 134.706G/s
UnaryFixture/BM_unary_relu_transpose/M:64/N:64/min_warmup_time:1.000_stddev 0.405 ns 0.417 ns 10 231.018M/s
UnaryFixture/BM_unary_relu_transpose/M:64/N:64/min_warmup_time:1.000_cv 0.17 % 0.17 % 10 0.17%
UnaryFixture/BM_unary_relu_transpose/M:512/N:512/min_warmup_time:1.000_mean 481150 ns 479519 ns 10 4.37974G/s
UnaryFixture/BM_unary_relu_transpose/M:512/N:512/min_warmup_time:1.000_median 483163 ns 481481 ns 10 4.35591G/s
UnaryFixture/BM_unary_relu_transpose/M:512/N:512/min_warmup_time:1.000_stddev 19118 ns 19053 ns 10 176.288M/s
UnaryFixture/BM_unary_relu_transpose/M:512/N:512/min_warmup_time:1.000_cv 3.97 % 3.97 % 10 4.03%
UnaryFixture/BM_unary_relu_transpose/M:2048/N:2048/min_warmup_time:1.000_mean 8770935 ns 8729697 ns 10 3.84785G/s
UnaryFixture/BM_unary_relu_transpose/M:2048/N:2048/min_warmup_time:1.000_median 8782429 ns 8746690 ns 10 3.83637G/s
UnaryFixture/BM_unary_relu_transpose/M:2048/N:2048/min_warmup_time:1.000_stddev 305062 ns 299606 ns 10 133.989M/s
UnaryFixture/BM_unary_relu_transpose/M:2048/N:2048/min_warmup_time:1.000_cv 3.48 % 3.43 % 10 3.48%
BM_unary_relu_transpose/M:50/N:50 kernel: \(126.4\) GiB/s
BM_unary_relu_transpose/M:64/N:64 kernel: \(134.7\) GiB/s
BM_unary_relu_transpose/M:512/N:512 kernel: \(4.379\) GiB/s
BM_unary_relu_transpose/M:2048/N:2048 kernel: \(3.847\) GiB/s